Distribusi normal terkait dengan distribusi probabilitas atau distribusi peluang yang menjadi pembahasan penting dalam bidang statistika. Distribusi normal adalah bagian penting dalam melakukan analisis data statistika karena dapat memberikan gambaran lebih jelas mengenai suatu fenomena di kehidupan.
Pengertian Distribusi Normal
Nama lain dari distribusi normal adalah distribusi Gauss atau Gaussian Distribution, yakni jenis fungsi peluang untuk peubah acak kontinu.
Distribusi normal dinamakan sebagai distribusi Gauss karena menyesuaikan dengan nama matematikawan Carl Friedrich Gauss asal Jerman yang mengembangkan fungsi Gauss.
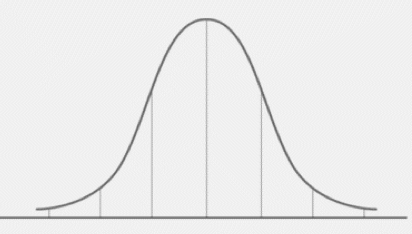
Fungsi Gauss sangat penting dalam ilmu Statistika karena dapat menggambarkan distribusi normal. Bentuk grafik fungsi Gauss adalah kurva melengkung seperti lonceng atau bell curve. Dengan adanya distribusi Gauss atau distribusi normal, maka penyebaran distribusi data dapat terlihat jelas.
Untuk menandai bahwa suatu distribusi tersebar merata, kurva distribusi Gauss akan memuncak di sisi tengahnya kemudian akan semakin melandai di kedua sisi kurva dengan persamaan nilai yang setara.
Bentuk kurva nilai dari peluang distribusi normal dipengaruhi oleh beberapa parameter yakni parameter nilai rata-rata (mean) dan parameter standar deviasi atau simpangan baku. Berikut penjelasan parameter pada distribusi Gauss:
1. Nilai mean atau rata-rata data dimanfaatkan sebagai pusat penyebaran nilai yang lain atau pusat distribusi. Nilai mean berguna sebagai penentu lokasi titik puncak pada suatu kurva lonceng. Sementara nilai di luar rata-rata dibuat menyebar di sekitar nilai rata-rata.
2. Parameter standar deviasi berguna untuk analisa variabilitas yang akan menentukan lebar sebuah kurva distribusi Gauss. Standar deviasi juga berguna dalam memperhitungkan jarak kecenderungan data akan melebar dari nilai mean yang merupakan titik pusat.
Apabila nilai standar deviasi semakin kecil, artinya bentuk kurva distribusi Gauss akan semakin menyempit alias meruncing. Dengan adanya standar deviasi, maka jarak antara rata-rata (mean) dengan data lainnya yang sedang dianalisa bisa terlihat jelas.
3. Untuk mendapatkan gambaran yang lebih detail mengenai populasi maka parameter yang digunakan adalah mean populasi μ dan deviasi standar populasi σ. Namun, penggunaan parameter populasi sangat sulit karena mengukur seluruh populasi hampir tidak mungkin dilakukan.
Oleh karena itu digunakan parameter rata-rata sampel x̅ dan parameter deviasi standar sampel (s).
Ciri-Ciri Distribusi Normal
- Titik puncak kurva distribusi normal terletak pada nilai mean atau nilai rata-rata. Nilai mean ada tepat di bagian tengah kurva distribusi normal. Sementara data distribusinya ada di sekitar nilai rata-rata atau titik puncak kurva tersebut
- Kurva distribusi Gauss atau distribusi normal dapat bersifat simetris berbentuk bell curve atau lonceng. Kurva distribusi normal sering disebut sebagai unimodal.
- Nilai rata-rata distribusi Gauss menentukan letak simetri dari kurva sementara simpangan baku atau standar deviasi menentukan penyebaran data.
- Total luas daerah yang ada di bawah kurva distribusi Gauss berjumlah 1, yakni terbagi merata di sisi kanan setengah dan sisi kiri setengah. Nilai ini berlaku untuk setiap distribusi probabilitas kontinu.
- Berdasarkan pembagian luas daerah distribusi Gauss, maka dapat disimpulkan bahwa setengah dari data populasi akan mempunyai nilai di bawah nilai rata-rata sementara sisanya memiliki nilai lebih besar dari rata-rata.
- Panjang dari ekor kurva distribusi Gauss dapat terus memanjang hingga tidak terbatas.
Penerapan Distribusi Normal
Distribusi normal digunakan untuk analisis data statistika variabel acak kontinu. Data yang awalnya tersebar acak akan dapat lebih mudah dibaca dan dianalisa. Oleh karena itu distribusi Gauss banyak diterapkan pada berbagai pemodelan dan perhitungan statistika seperti:
- Perhitungan dan analisa error measurement
- Kumpulan data tekanan darah masyarakat di suatu daerah
- Kumpulan data tinggi badan siswa atau pelajar sekolah
- Kumpulan data berat badan pelajar sekolah
Data-data yang diambil secara acak di atas kemudian dikumpulkan dan diolah menggunakan distribusi normal sehingga tampak nilai rata-rata normal dan mana saja yang termasuk outlier (di luar batas standar).
Sebagai contoh, standar normal minimum tinggi badan pelajar kelas 6 SD adalah 135 cm, maka dari distribusi normal pelajar suatu daerah bisa dilihat apakah tinggi badan kebanyakan mereka sudah memenuhi standar atau di bawah tinggi standar.
Dengan distribusi normal, maka objektivitas penilaian akan semakin baik. Hal ini karena distribusi simetris pada nilai rata-rata semua data di populasi tertentu maka penilaian dapat dilakukan secara adil dan tidak berat sebelah.
Tabel Z Distribusi Normal
Tabel berisi variabel Z merupakan nilai transformasi dari distribusi normal yang memiliki simpangan baku σ dan peubah acak X = μ ke distribusi normal baku. Oleh karena itu tabel Z sangat dibutuhkan dalam nenentukan distribusi probabilitas dari distribusi normal.
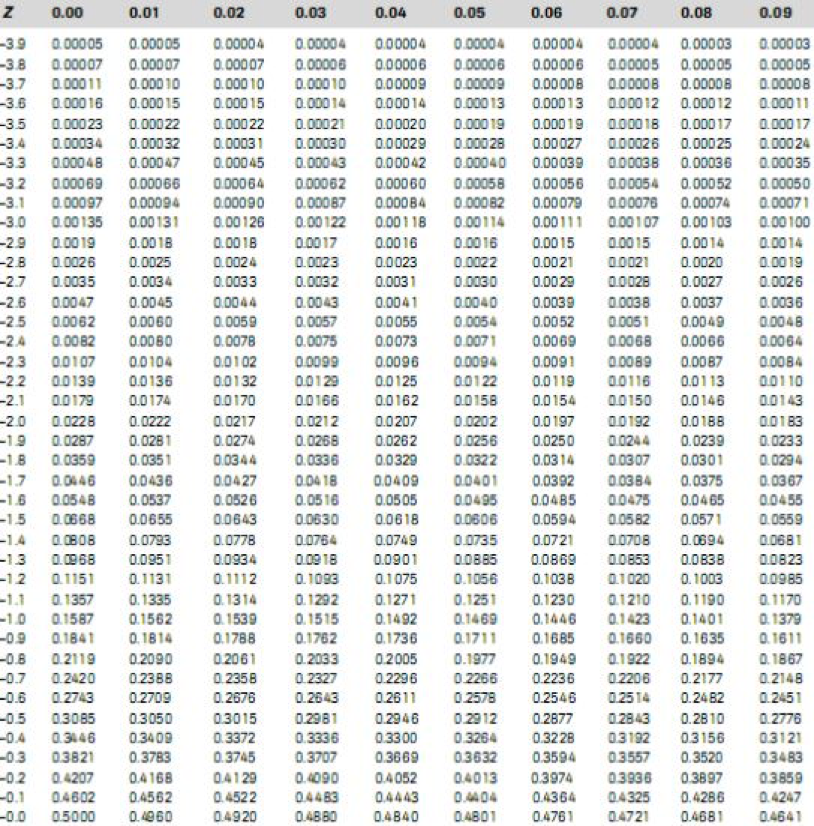
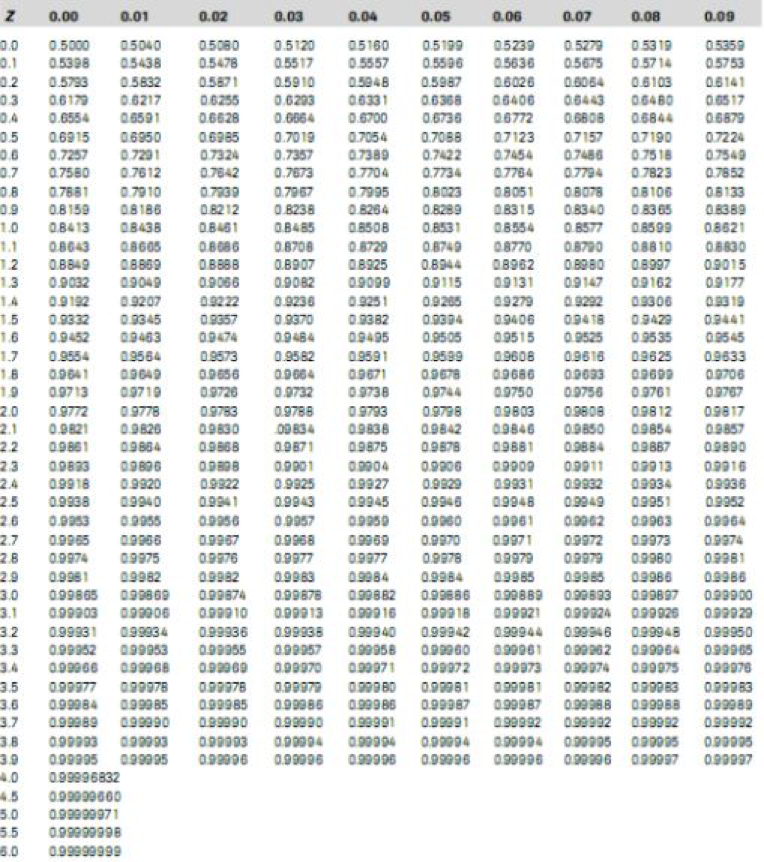
Tabel di atas menunjukkan tabel Z distribusi normal yang memiliki acuan pada kolom dan juga barisnya. Acuan pada kolom dan baris berguna dalam menentukan nilai z. Skor z ini mewakili jumlah dari deviasi standar di sisi bawah atau sisi atas.
Langkah untuk menentukan nilai skor z:
- Lihat bagian kolom awal. Sebagai contoh nilai skor z yang ingin ditentukan adalah 1,36. Maka tahap pertama yang harus dilakukan adalah mencari di baris 1,3
- Selanjutnya amati baris awal. Cari baris nilai 0,06
- Carilah sel yang menjadi titik pertemuan antara kolom dan baris yang dicari di langkah pertama dan kedua. Nilai skor z untuk 1,36 adalah 0,9131
Contoh Soal Distribusi Kelompok
Pada ujian penerimaan mahasiswa baru di universitas X, diketahui ada 1200 calon mahasiswa baru yang mendaftar dan mengikuti ujian penerimaan mahasiswa baru. Rata-rata hasil nilai ujian calon mahasiswa baru adalah 67 dengan simpangan baku hasil tes sebesar 10.
Apabila diketahui data nilai hasil ujian penerimaan mahasiswa baru terdistribusi normal, tentukan berapa persen calon mahasiswa baru yang memperoleh nilai A apabila syarat memperoleh nilai A yaitu nilai ujian harus lebih dari 80.
Diketahui:
σ = 10
μ = 67
x = 80
Jawab:
Yang diminta adalah nilai Z (X > 80), sehingga rumus yang digunakan sebagai berikut:
Z (X > 80) = 1 – Z (X < 80)
Pertama-tama dihitung terlebih dahulu nilai Z (X < 80)
Z = (x – μ)/σ
Z = (80 – 67)/10
Z = 13/10 = 1,3
Selanjutnya dicari nilai Z untuk 1,3 melalui tabel Z. Diperoleh nilai Z untuk 1,3 adalah 0,9032 sehingga jumlah persentase calon mahasiswa baru yang mendapat nilai A adalah:
Z (X > 80) = 1 – Z (X < 80)
Z (X > 80) = 1 – 0,9032
Z (X > 80) = 0,0968
Z (X > 80) = 9,68%
Distribusi normal atau distribusi Gauss adalah jenis distribusi yang digunakan dalam ilmu statistika untuk menggambarkan sebaran variabel acak kontinu. Bentuk grafik pada distribusi Gauss menyerupai bentuk lonceng dengan titik puncak adalah nilai rata-rata data (mean).
