Mempelajari konsep peluang sangat penting mengingat perannya yang besar dalam kehidupan sehari-hari. Teori peluang banyak digunakan di berbagai bidang mulai dari ekonomi, pendidikan, kesehatan, sosial, olahraga dan lainnya.
Definisi Peluang Matematika
Istilah peluang tentu sangat sering terdengar ketika berbicara mengenai kemungkinan suatu hal dapat terjadi. Sebagai contoh saat pertandingan olahraga, seringkali terdengar prediksi para ahli yang mengatakan peluang suatu tim untuk memenangkan pertandingan sangat kecil atau sangat besar.
Dapat disimpulkan bahwa peluang dalam Matematika memiliki arti kebolehjadian atau probabilitas suatu kejadian akan benar terjadi. Peluang dapat ditunjukkan menggunakan angka yang bersifat objektif dan terukur seperti “peluang terjadinya hujan sekitar 35%”.
Peluang juga dapat ditunjukkan menggunakan kalimat yang sifatnya subjektif dan kurang terukur seperti “Peluang tim sepakbola Indonesia memenangkan pertandingan cukup besar”. Kata “cukup besar” menunjukkan peluang meski tidak jelas ukuran yang dikatakan besar tersebut.
Besar peluang selalu dinyatakan dengan bilangan di antara 0 sampai 1. Angka 0 menyatakan bahwa peluang suatu peristiwa tidak mungkin terjadi sementara angka 1 menyatakan bahwa peluang suatu peristiwa pasti terjadi. Jika peluang kejadian adalah P(K), maka besar peluang dinyatakan berikut ini:
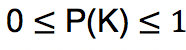
Ada beberapa istilah yang sering digunakan dalam materi peluang yang harus dipahami yakni ruang sampel, titik sampel dan kejadian. Ruang sampel atau ruang contoh terdiri dari himpunan semua hasil yang mungkin muncul pada sebuah percobaan. Ruang sampel disimbolkan sebagai S.
Titik sampel juga dikenal sebagai titik contoh merupakan anggota-anggota yang ada di ruang sampel. Kejadian adalah himpunan bagian dari suatu ruang sampel.
Pelajari Juga Himpunan
Rumus Peluang
Saat dilakukan percobaan pelemparan uang koin, frekuensi munculnya gambar akan menurun atau membesar secara relative seiring dengan semakin banyaknya percobaan dilakukan. Saat percobaan dilakukan sebanyak kurang dari 5 kali, maka frekuensi relatif bisa mendekati 1 atau bahkan mendekati 0.
Namun, tatkala percobaan dilakukan semakin banyak, frekuensi relatif akan semakin mendekati 0,5, ditulis P (A) = 0,5, dengan perbedaan nilai yang relatif tidak terlalu jauh. Peluang munculnya angka merupakan limit frekuensi relatif pada banyak percobaan n yang mendekati tidak terhingga.
Oleh karena itu, rumus peluang dapat ditulis sesuai dengan definisi empirisnya sebagai berikut:
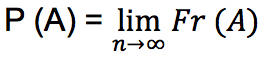
Apabila ruang sampel percobaan ditulis dengan S, yang mana masing-masing anggota dari ruang sampel S memiliki kesempatan yang sama untuk bisa muncul, maka peluang A terjadi menggunakan rumus berikut:
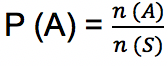
Keterangan:
n (A) = banyak anggota kejadian A
n (S) = banyak anggota ruang sampel S
Kejadian Majemuk
Kejadian majemuk adalah kejadian yang terdiri dari beberapa titik sampel yang dioperasikan sehingga membentuk suatu kejadian yang baru. Kejadian majemuk juga didefinisikan sebagai percobaan atau kejadian yang terjadi sebanyak lebih dari sekali.
Kejadian Komplemen
Kejadian komplemen A adalah seluruh kejadian yang tidak termasuk kejadian A tersebut. Kejadian komplemen A ditulis sebagai A’ memenuhi persamaan berikut:
P (A) + P (A’) = 1, bisa juga ditulis sebagai
P (A’) = 1 – P (A)
Penjumlahan Peluang
- Kejadian Saling Lepas
Kejadian saling lepas atau mutually exclusive adalah kejadian pada ruang sampel yang mana kejadian-kejadian tersebut tidak saling berhubungan maka

Pada ruang sampel yang mana kejadian-kejadian di dalamnya saling lepas, maka peluang A atau B dirumuskan dengan persamaan berikut ini:
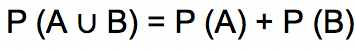
Persamaan di atas disebut sebagai aturan penjumlahan dalam peluang kejadian majemuk saling lepas.
- Kejadian Tidak Saling Lepas
Dua kejadian disebut sebagai kejadian tidak saling lepas apabila ada setidaknya satu elemen dari salah satu kejadian yang juga termasuk elemen dari kejadian lainnya. Kejadian tidak saling lepas dirumuskan dengan

dibaca sebagai peluang kejadian A atau kejadian B.
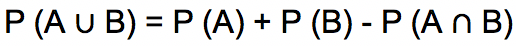
- Kejadian Saling Bebas
Kejadian saling bebas stokastik adalah kejadian-kejadian yang muncul pada ruang sampel namun kejadian satu dan lainnya tidak saling mempengaruhi. Pada kejadian saling bebas stokastik terdapat aturan perkalian untuk menghitung peluang terjadinya kejadian A dan B sekaligus, dinotasikan dengan

Dan cara menghitungnya dengan persamaan berikut ini:
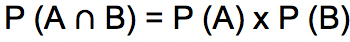
Contoh kejadian saling bebas adalah pada pelemparan sebuah dadu dan koin. Hasil yang keluar pada dadu dan koin tidak mempengaruhi satu dengan lainnya.
- Kejadian Bersyarat
Kejadian bersyarat adalah kejadian yang terjadi apabila kejadian lainnya telah diketahui atau telah terjadi terlebih dulu sehingga kejadian bersyarat B terhadap A ditulis dengan notasi P (B | A).
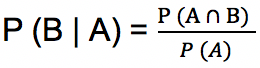
Contoh kejadian bersyarat adalah pada pengambilan kelereng dari dalam kotak. Apabila kelereng di dalam kotak terdiri dari 5 kelereng merah dan 5 kelereng biru. Maka ketika diambil sebuah kelereng dari dalam kotak dan tidak dikembalikan, kemudian kelereng terus diambil.
Pengambilan kelereng yang kedua dipengaruhi oleh pengambilan kelereng sebelumnya sehingga disebut sebagai kejadian bersyarat.
Pelajari Juga Permutasi & Kombinasi
Contoh Soal Peluang
- Soal 1
Sebuah kotak memiliki 3 bola pink dan 1 bola hitam. Dari dalam kotak tersebut diambil bola secara acak sebanyak 3 sekaligus. Tentukan peluang terambilnya ketiga bola terdiri atas:
a. Salah satu bola berwarna hitam
b. Ketiga bola terambil berwarna pink
Jawab:
Jika diibaratkan bahwa tiga bola pink disimbolkan dengan P1, P2, P3 dan bola hitam adalah H, maka ada 4 kemungkinan pengambilan bola dari dalam kotak yakni:
P1 P2 H
P1 H P3
P2 H P3
P1 P2 P3
Ruang sampel dari kasus ini adalah n (S) = 4
a. Apabila kejadian A adalah terambilnya salah satu bola berwarna hitam, maka banyak terjadinya A, n (A) = 3. Peluang terambilnya salah satu bola berwarna hitam:
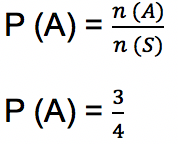
b. Peluang ketiga bola terambil berwarna pink, n (B) = 1, sehingga:
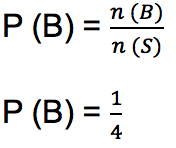
- Soal 2
Diketahui suatu kotak mempunyai 11 bola yang terdiri dari 6 bola hijau dan 5 bola ungu. Setiap pengambilan satu bola, maka bola tersebut tidak dikembalikan lagi ke dalam kotak. Tentukan berapa peluang terjadinya pengambilan bola hijau diikuti bola ungu berturut-turut.
Jawab:
Peluang terambilnya hijau pada pengambilan pertama adalah:
P (H) = 6/11
Banyak bola setelah pengambilan pertama adalah 10, sehingga P (U | H) = 5/10 = ½
Sehingga,
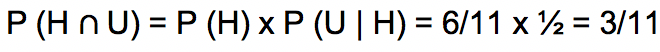
Baca Juga : Kumpulan Contoh Soal Peluang & Pembahasannya
Kesimpulan
Teori peluang berawal dari sebuah permainan judi yang mana para pemain ingin mengetahui berapa besar kemungkinan mereka memenangkan suatu pertaruhan. Meski begitu, ternyata konsep peluang sangat bermanfaat dalam berbagai bidang lainnya seperti prediksi ekonomi, bisnis, kesehatan dan sebagainya.
