Persamaan kuadrat adalah persamaan yang mempunyai variabel pangkat dua. Koefisien variabel berpangkat 2 pada persamaan kuadrat tidak boleh sama dengan 0. Persamaan kuadrat sangat membantu dalam perhitungan yang melibatkan gerak benda ataupun desain bangunan berbentuk parabola.
Pengertian Persamaan Kuadrat
Persamaan kuadrat dalam x merupakan sebuah persamaan yang memiliki bentuk ax² + bx + c = 0 yang mana a, b dan c merupakan bilangan real dengan a ≠ 0.
Persamaan kuadrat mempunyai beberapa ciri-ciri sebagai berikut:
- Persamaan kuadrat berbentuk persamaan yang ruas kanan dan kirinya dihubungkan dengan notasi sama dengan “=”
- Pangkat tertinggi dari variabel atau peubahnya adalah 2 dengan pangkat terendah berupa nol
- Koefisien dari variabel dengan pangkat dua tidak boleh sama dengan 0
- Koefisien variabel berpangkat 1 dan juga 0 boleh bernilai 0
- Nilai Koefisien variabel harus berupa bilangan real
Koefisien variabel berpangkat 2 pada persamaan kuadrat tidak boleh sama dengan 0 karena menyebabkan persamaan tersebut tidak lagi menjadi persamaan kuadrat. Misal persamaan 3x + 5 = 0 adalah persamaan linear, bukan persamaan kuadrat sebab koefisien variabel berpangkat 2 sama dengan 0.
Persamaan Kuadrat dalam Kehidupan Nyata
Persamaan kuadrat mempunyai banyak manfaat dalam kehidupan nyata. Sebagai contoh perhitungan kecepatan gerak lintasan proyektil atau bola pada lintasan berbentuk parabola bisa dihitung dengan menggunakan persamaan kuadrat.
Persamaan kuadrat akan membantu untuk menghitung puncak tertinggi dari gerak benda yang dilempar pada lintasan berbentuk parabola. Persamaan kuadrat juga berfungsi dalam perhitungan desain arsitektur berbentuk lengkungan seperti tiang jembatan, atap bangunan dan lainnya.
Persamaan dan Fungsi Kuadrat
ax² + bx + c = 0
Keterangan:
a = koefisien x²
b = koefisien x
c = konstanta persamaan
x = variabel atau peubah
Pelajari Juga Fungsi Kuadrat
Rumus Persamaan Kuadrat
1. Jumlah akar persamaan kuadrat:
x1 + x2 = -b/a
2. Hasil kali persamaan kuadrat:
x1 . x2 = c/a
Akar-Akar Persamaan Kuadrat
Akar persamaan kuadrat adalah penyelesaian dari persamaan kuadrat berupa harga x yang memenuhi persamaan. Solusi akar persamaan kuadrat ditentukan oleh nilai diskriminan dari persamaan kuadrat yakni D = b² – 4ac.
a. Apabila nilai D < 0, maka persamaan kuadrat tidak memiliki akar nyata atau hanya memiliki akar imajiner
b. Apabila nilai D = 0, maka akar persamaan kuadrat berbentuk akar kembar atau dua akarnya sama.
c. Apabila nilai D > 0, maka persamaan kuadrat memiliki dua akar nyata atau real.
Untuk mencari akar persamaan kuadrat bisa melalui cara pemfaktoran, melengkapkan kuadrat sempurna hingga rumus ABC.
- Metode Pemfaktoran
Metode pemfaktoran dengan memfaktorkan hasil kali dari koefisien a dan c serta nilai koefisien b. Perhatikan contoh pemfaktoran berikut ini:
x² – x – 6 = 0
Hasil kali a x c = -6
b = -1
Cari bilangan yang apabila dikali = -6 jika ditambah = -1, yakni 2 dan -3. Masukkan 2 dan -3 ke dalam persamaan kuadrat:
x² – 3x + 2x – 6 = 0
x (x – 3) + 2 (x – 3) = 0
(x + 2) (x – 3) = 0
Sehingga x yang memenuhi adalah x = -2 atau x = 3
- Metode Melengkapkan Kuadrat Sempurna
Bentuk umum persamaan kuadrat ax² + bx + c = 0 dengan koefisien a, b serta koefisien c berupa bilangan real serta nilai a tidak sama dengan 0. Jika a = 1, maka untuk mencari akar persamaan kuadrat dengan metode melengkapkan kuadrat sempurna sebagai berikut:
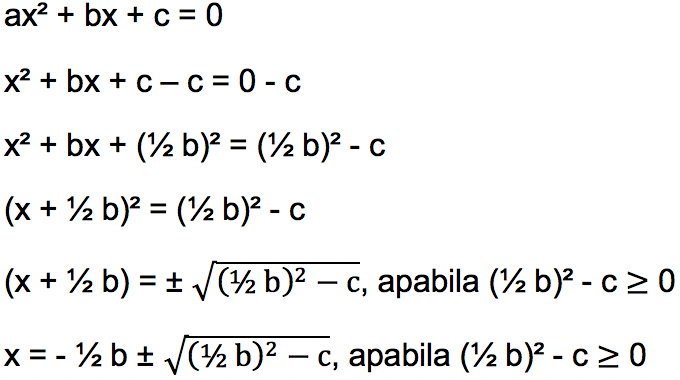
Contoh penggunaan metode melengkapkan kuadrat sempurna untuk mencari akar persamaan kuadrat
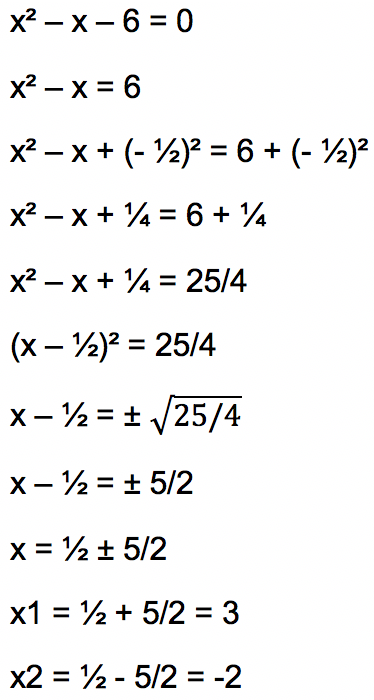
Sehingga akar persamaan kuadrat x² – x – 6 = 0 adalah 3 dan -2.
- Metode Rumus ABC
Terkadang mencari akar persamaan kuadrat dengan menggunakan rumus di atas sedikit sulit terutama jika koefisien pada persamaan kuadrat bernilai besar. Untuk mencari akar persamaan kuadrat lebih mudah dengan rumus ABC di bawah ini:
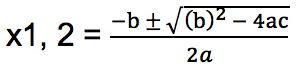
Rumus ABC di atas berlaku untuk persamaan kuadrat ax² + bx + c = 0 dengan koefisien a, b dan c merupakan bilangan real serta nilai a ≠ 0.
Pelajari Juga Kumpulan Contoh Soal Persamaan Kuadrat & Pembahasan
Contoh Soal Persamaan Kuadrat
Soal:
Seorang penjual mesin pompa air sudah merakit mesin pompa air dengan biaya yang dikeluarkan selama satu bulan sebanyak Rp 37.500.000. Hasil rakitan mesin pompa airnya selama satu bulan dijual ke pasaran dan berhasil terjual hingga hanya tersisa sebanyak 3 unit saja.
Apabila hasil penjualan mesin pompa air meraup keuntungan per unitnya sebesar Rp 500.000 dengan hasil penjualan mencapai Rp 36.000.000. Tentukan berapa banyak mesin pompa air yang berhasil diproduksi selama satu minggu.
Jawab:
Pertama-tama dimisalkan terlebih dahulu bahwa banyak mesin pompa air yang dirakit dalam sebulan adalah h, maka:

Untuk menghitung berapa harga jual setiap unit mesin pompa air adalah dengan membagi hasil penjualan mesin pompa air dengan jumlah yang terjual. Jumlah yang terjual adalah h – 3 (tersisa 3 unit pompa). Maka harga jual setiap unit mesin pompa air sebesar
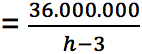
Untung yang diperoleh sama dengan harga jual barang (Hj) dikurangi biaya modal (Hm) atau biaya perakitan barang.
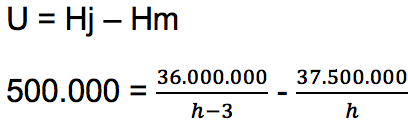
(kedua ruas dibagi 500.000)
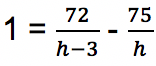
(Penyebut pada pecahan di sisi kanan disamakan dengan menjadikannya sebagai h (h – 3))
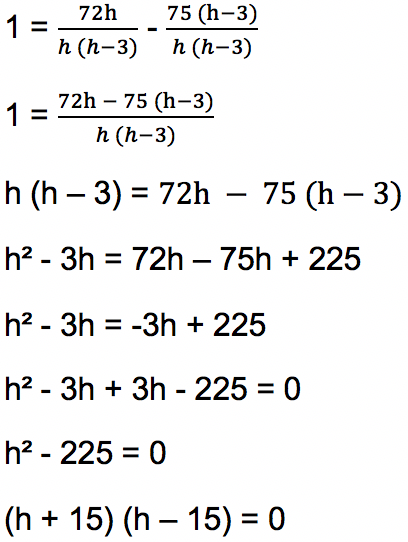
Sehingga solusi dari persamaan kuadrat h² – 225 = 0 adalah h = -15 atau h = 15. Karena solusi h = -15 tidak mungkin sebab yang ditanyakan adalah jumlah unit mesin pompa air yang diproduksi maka jawaban yang benar adalah h = 15 atau 15 unit.
