Materi mengenai standar deviasi masuk ke dalam salah satu konsep penting yang diajarkan di dalam ilmu statistika bersamaan dengan materi mean, median dan modus. Standar deviasi digunakan untuk menjelaskan penyebaran data yang terjadi dan estimasi tingkat keakurasian pengukuran.
Pengertian Standar Deviasi
Istilah standar deviasi dalam ilmu statistika dikeluarkan oleh ahli matematika dari Jerman yakni Karl Ganss yang saat itu mempelajari tingkat penyebaran dari berbagai jenis data. Karl Ganss kemudian mengeluarkan istilah deviasi standar atau standar deviasi untuk memberikan gambaran terkait penyebaran yang ada.
Pada hari ini, ilmu tentang standar deviasi sangat penting terutama pada penelitian yang dilakukan oleh ilmuwan untuk menunjukkan tingkat keakurasian pengukuran yang dilakukan. Standar deviasi juga dikenal sebagai simpangan baku
Standar deviasi atau simpangan baku disajikan dalam rangka mengatasi kelemahan yang ada pada rataan simpangan. Rataan simpangan memiliki fungsi yang hampir sama dengan standar deviasi, yakni memberi gambaran mengenai penyebaran yang ada serta menunjukkan tingkat keakurasian data.
Namun, rataan simpangan bekerja pada bilangan berharga mutlak sehingga data yang memiliki rentang lebih besar atau lebih kecil tidak terlihat bedanya. Oleh karena itu digunakan konsep simpangan baku atau standar deviasi yang dinotasikan dengan S.
Standar deviasi merupakan akar dari varians suatu data, baik itu data berkelompok maupun data tunggal.
Cara Menghitung Standar Deviasi
Menghitung standar deviasi dibedakan berdasarkan jenis datanya apakah data yang digunakan dalam bentuk data tunggal atau data kelompok. Tata cara menghitung standar deviasi dari data tunggal menggunakan langkah-langkah di bawah ini:
- Pertama-tama cari nilai rerata atau mean dari data tunggal terlebih dahulu dengan rumus Mean
- Hitung selisih semua data tunggal dengan nilai Mean kemudian hasil pengurangan dikuadratkan
- Jumlahkan semua nilai pengurangan yang sudah dikuadratkan dan dibagi banyak data
- Nilai yang diperoleh diakar kuadrat
Jika data yang akan dihitung merupakan data terkelompok, maka untuk menghitung standar deviasi menggunakan langkah berikut ini:
- Pertama-tama cari nilai rerata atau mean dari data kelompok
- Hitung selisih semua nilai tengah data dengan nilai rerata kemudian hasil pengurangan dikuadratkan
- Kalikan hasil kuadrat pengurangan dengan frekuensi dari kelas interval ke-i.
- Jumlahkan semua nilai dan dibagi banyak data
- Nilai yang diperoleh diakar kuadratkan
Rumus Standar Deviasi
- Menghitung Standar Deviasi Data Tunggal
Untuk menghitung standar deviasi dari data tunggal dilakukan dengan menghitung nilai akar dari varians atau ragamnya. Rumus varians dari kumpulan data tunggal adalah:
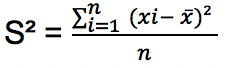
Simpangan baku atau standar deviasi adalah akar dari variansnya sehingga rumus standar deviasi menjadi:
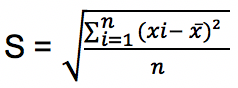
Rumus simpangan baku di atas berlaku untuk n > 30 atau merupakan data populasi. Sementara jika simpangan baku yang dihitung adalah data sampel dengan n < 30, maka rumus yang digunakan sebagai berikut:
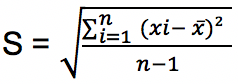
- Menghitung Standar Deviasi Data Terkelompok
Apabila data yang disediakan dalam bentuk distribusi frekuensi atau data terkelompok, maka cara mencari standar deviasi adalah dengan melibatkan elemen frekuensi dari kelas interval yang sedang dicari (fi). Berikut rumus simpangan bakunya:
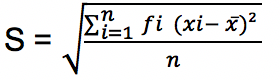
Patut dicatat bahwa rumus simpangan baku data terkelompok di atas digunakan untuk n > 30 atau merupakan data populasi. Untuk n < 30 atau merupakan data sampel maka digunakan rumus di bawah ini:
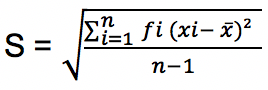
Keterangan:
S = simpangan baku atau standar deviasi

xi = titik tengah yang ada di kelas interval ke-i
fi = frekuensi dari kelas interval ke-i
Standar Deviasi Excel
Perhitungan standar deviasi dari banyak data saat ini banyak yang dikerjakan melalui komputer, salah satunya adalah melalui software Microsoft Excel. Cara menghitung standar deviasi pada Excel bisa dilakukan baik secara semi manual maupun otomatis.
Apabila menggunakan cara semi manual, itu artinya pengguna Excel masih harus memasukkan rumus perhitungan ke dalam kolom-kolom tabel Microsoft Excel secara manual. Sementara cara otomatis adalah menggunakan perintah bawaan dari Excel untuk mengerjakaan standar deviasi.
Di bawah ini panduan menghitung standar deviasi Excel melalui cara otomatis:
- Pertama-tama input data pada Microsoft Excel secara lengkap
- Selanjutnya blok data-data yang sudah diinputkan
- Gunakan fungsi STDEV.S (Number 1: Number i), Number i merupakan elemen paling akhir dari data-data yang ada
Pelajari Juga Mean, Median, Modus
Contoh Soal dan Pembahasannya
- Soal 1
Diketahui ada beberapa data yang tersebar terdiri dari 47, 42, 39, 45, 40, 32, 35,
Tentukan berapakah besar ragam atau varians dan standar deviasinya.
Jawab:
Untuk menghitung standar deviasi dan variansnya, pertama-tama dihitung terlebih dahulu nilai mean atau rerata dari data tersebut.
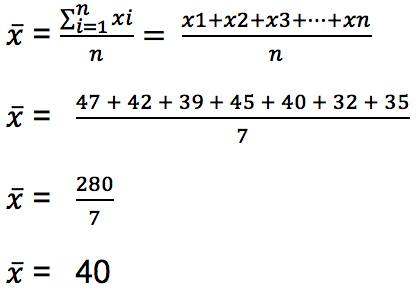
Sehingga nilai rerata dari data di atas adalah 40. Selanjutnya menghitung standar deviasi dan varians. Standar deviasi merupakan akar dari besar varians sehingga pertama-tama bisa dihitung nilai varians dari sebaran data di atas menggunakan rumus berikut:
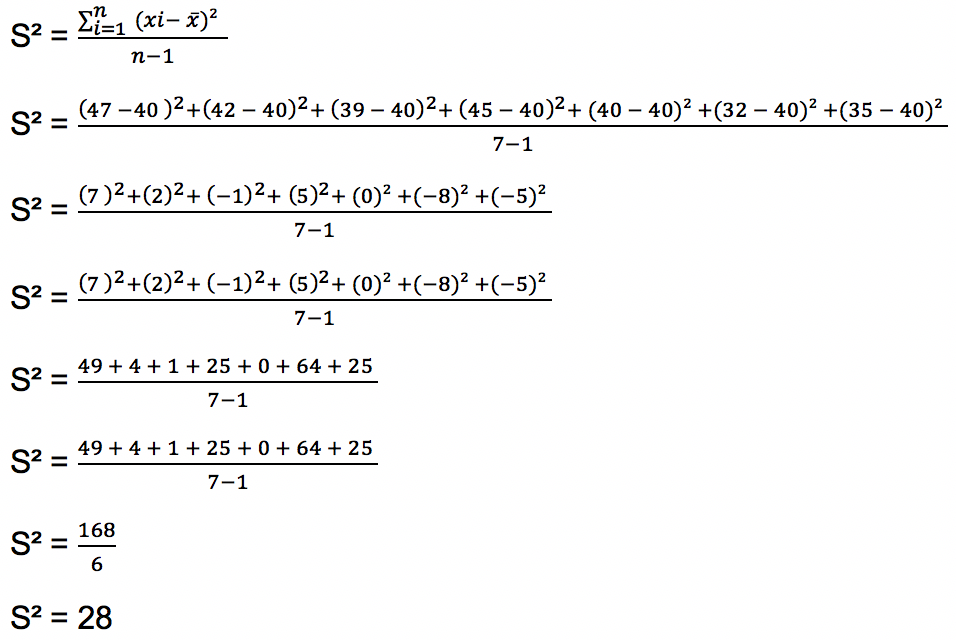
Selanjutnya dihitung standar deviasi data tersebar di atas dengan mengakarkan nilai varians.
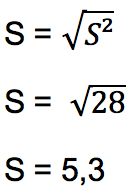
- Soal 2
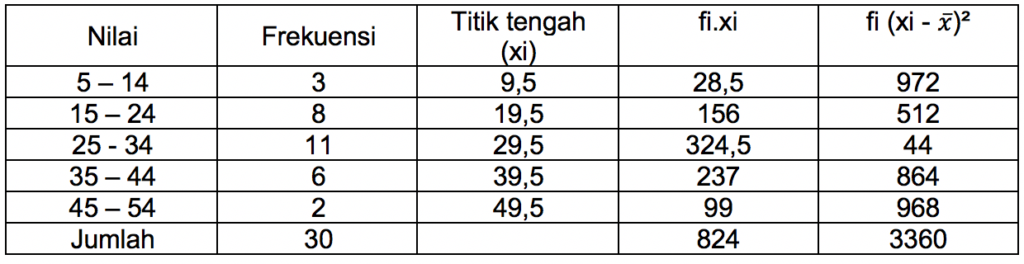
Hasil tes Bahasa Inggris 30 siswa kelas X seperti ditunjukkan pada tabel di bawah ini. Tentukan berapakah standar deviasi atau simpangan bakunya.
| Nilai | Frekuensi |
| 5 – 14 | 3 |
| 15 – 24 | 8 |
| 25 – 34 | 11 |
| 35 – 44 | 6 |
| 45 – 54 | 2 |
Jawab:
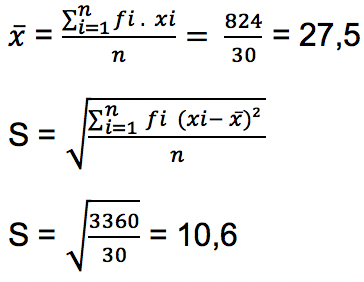
Kesimpulan
Standar deviasi merupakan akar dari nilai varians dari kumpulan beberapa data. Standar deviasi juga disebut sebagai simpangan baku memberikan solusi atas kelemahan dari rataan simpangan. Standar deviasi digunakan dalam menunjukkan tingkat keakurasian perhitungan pada penelitian.
