Materi relasi dan fungsi dalam Matematika menggambarkan hubungan yang terbentuk antara himpunan asal ke himpunan kawannya. Dengan adanya aturan relasi dan juga fungsi maka pembaca bisa mengetahui aturan yang mengikat kedua himpunan yang diberikan.
Pengertian Relasi dan Fungsi
- Pengertian Relasi
Istilah relasi dan fungsi adalah salah satu cabang dalam Matematika yang digunakan untuk menunjukkan hubungan antara kelompok yang ada. Relasi merupakan aturan pemasangan atau pengaitan antara anggota-anggota suatu himpunan ke anggota yang ada di himpunan lainnya.
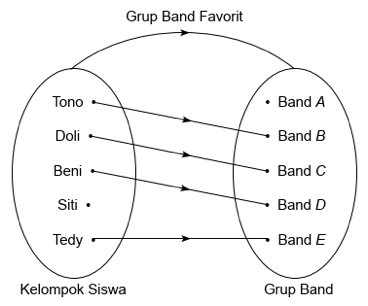
Gambar 1 di atas menunjukkan dua buah himpunan yang mana himpunan di sisi kiri adalah himpunan berisi sekelompok siswa dan himpunan di sebelah kanan adalah nama-nama group band. Antara himpunan kelompok siswa dan grup band dihubungkan oleh tanda panah “Grup Band Favorit”.
Dengan adanya tanda panah tersebut maka pembaca bisa menemukan beberapa fakta seperti:
- Tedy mempunyai grup band favorit yakni Band E
- Doli mempunyai grup band favorit yakni Band C
- Beni mempunyai grup band favorit yakni Band D, dan seterusnya
Tanda panah bertuliskan “Grup Band Favorit” adalah relasi yang menghubungkan dari kelompok siswa menuju kelompok grup band. Bentuk relasi seperti ini adalah relasi dengan diagram panah. Relasi dapat dinyatakan dalam beberapa bentuk seperti himpunan pasangan terurut hingga diagram kartesius.
Dapat disimpulkan bahwa ada dua syarat yang membuat relasi dapat terbentuk yakni:
- Relasi bisa terbentuk jika ada dua kelompok atau himpunan yang mempunyai anggota yang dipasangkan satu dengan himpunan lainnya. Pada Gambar 1 terlihat bahwa himpunan pertama adalah kelompok siswa dan himpunan kedua adalah grup band.
- Relasi bisa terbentuk jika terdapat aturan yang menghubungkan antara anggota himpunan satu dengan anggota himpunan lainnya. Pada Gambar 1 aturan yang menghubungkan kedua himpunan adalah “Grup Band Favorit”
Himpunan yang anggotanya akan dipasangkan disebut sebagai daerah asal atau domain. Sementara himpunan yang anggotanya berpasangan dengan himpunan asal disebut kodomain. Daerah hasil atau range adalah himpunan yang anggotanya terdiri dari daerah kodomain yang berpasangan dengan domain.
Berdasarkan Gambar 1, himpunan siswa adalah daerah asal atau domain. Himpunan grup band merupakan kodomain dan daerah hasil atau range yakni band B, band C, band D, band E.
- Pengertian Fungsi
Fungsi adalah salah satu bagian dari relasi dalam Matematika namun tidak semua relasi termasuk fungsi. Syarat suatu relasi dapat disebut sebagai fungsi meliputi dua syarat yakni:
- Seluruh anggota himpunan asal (domain) mempunyai pasangan dengan anggota himpunan kawan atau kodomain
- Seluruh anggota himpunan asal (domain) mempunyai pasangan tunggal dengan anggota himpunan kawan atau kodomain. Namun himpunan kodomain bisa saja berpasangan dengan lebih dari satu anggota di himpunan asal (domain).
Sehingga bisa disimpulkan bahwa fungsi f dari himpunan A (domain) ke himpunan B (kodomain) yakni aturan pengaitan (relasi) yang memasangkan setiap satu anggota himpunan A (asal atau domain) dengan tepat satu anggota yang ada di himpunan B (kodomain).
Penulisan fungsi dalam relasi himpunan A ke B bisa dituliskan menjadi f : A → B. Cara membaca notasi fungsi tersebut adalah fungsi f memetakan setiap anggota himpunan dari A tepat satu ke anggota himpunan B.
Apabila f memetakan suatu elemen dengan x A ke himpunan y B disebutkan bahwa y merupakan peta dari x oleh fungsi f. Peta tersebut dituliskan dengan notasi f(x) yang mana x disebut prapeta y, sehingga fungsi f : x → y dibaca sebagai fungsi f yang memetakan x ke y sedemikian hingga y = f(x).
Grafik Fungsi
Fungsi dapat dibedakan ke dalam tiga jenis yakni fungsi konstan (fungsi tetap), fungsi linear dan juga fungsi kuadrat. Fungsi tetap merupakan fungsi dengan nilai f(x) atau daerah hasil bersifat tetap (konstan) untuk berapapun nilai x.
Fungsi linear yakni fungsi yang dirumuskan dengan persamaan f(x) = ax + b. Nilai a tidak boleh 0 dengan b merupakan bilangan konstan bisa berupa 0. Grafik yang terbentuk oleh fungsi linear adalah garis lurus.
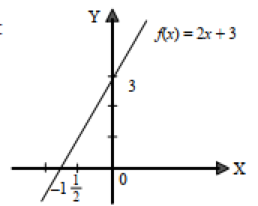
Grafik Fungsi Kuadrat
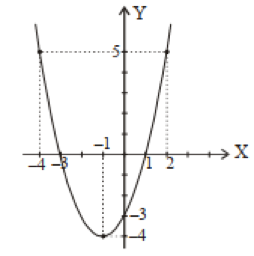
Fungsi kuadrat merupakan salah satu bentuk fungsi yang dirumuskan dengan persamaan kuadrat f(x) = ax² + bx + c, yang mana variabel a tidak boleh sama dengan 0 serta variabel a, b serta c merupakan bilangan konstan.
Grafik yang terbentuk dari fungsi kuadrat adalah parabola seperti yang tampak di Gambar 3.
Contoh Soal Relasi dan Fungsi
Diketahui suatu fungsi f : x → f(x) dengan rumus fungsi f(x) = hx – i. Apabila f(4) = 3 dan f(2) = -1 tentukanlah berapa nilai h dan i serta tuliskan bagaimana rumus fungsinya.
Diketahui:
f(x) = hx – i
f(4) = 3
f(2) = -1
Jawab:
Apabila f(4) = 3 sehingga f(x) = hx – i → 3 = 4h – i … (i)
Apabila f(2) = -1 sehingga f(x) = hx – i → -1 = 2h – i … (ii)
Selanjutnya terapkan metode eliminasi pada dua persamaan di atas yakni persamaan (i) dan persamaan (ii).
3 = 4h – i
-1 = 2h – i
___________-
3 – (-1) = 4h – 2h
4 = 2h
h = 4/2 = 2
Setelah diperoleh nilai h adalah 2 maka dapat disubstitusikan ke dalam salah satu persamaan (i) atau persamaan (ii). Untuk kasus ini dipilih persamaan (ii) yakni -1 = 2h – i. Sehingga didapatkan:
-1 = 2h – i
-1 = 2 x (2) – i
-1 = 4 – i
i = 4 + 1
i = 5
Sehingga diperoleh nilai variabel i = 5 dan variabel h = 2
Berdasarkan nilai variabel h dan i maka rumus fungsi f(x) = hx – i dapat dituliskan menjadi f(x) = 2x – 5
Fungsi Invers
Seluruh himpunan yang dipetakan oleh fungsi pasti memiliki invers yang bisa berbentuk fungsi ataupun bukan fungsi. Invers adalah kebalikan atau pasangan yang ditukarkan dari suatu fungsi. Apabila fungsi dituliskan dengan f(x), maka inversnya menjadi f-1(x).
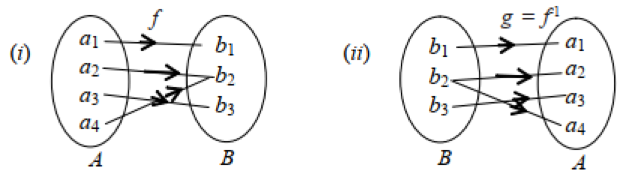
Contoh Soal Fungsi Invers
Diketahui fungsi H(x) = 5x + 10. Tentukan fungsi invers H-1(x).
Jawab:
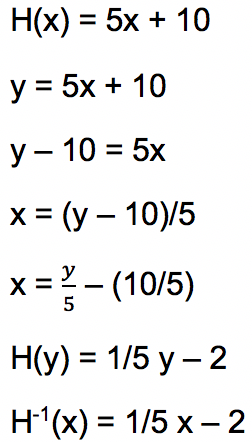
Kesimpulan
Mempelajari materi relasi dan fungsi sangat penting untuk melatih kemampuan dalam memetakan suatu hubungan yang terbentuk antara masing-masing anggota dua buah himpunan. Di kehidupan nyata, kemampuan mencari fungsi yang terbentuk antara dua himpunan data sangat penting dalam sebaran data.
