Deret Geometri Tak Hingga: Pengertian, Rumus, Contoh Soal & Pembahasan

Barisan geometri merupakan barisan bilangan dengan nilai pembading atau rasio dari dua suku berurutan bernilai tetap. Deret geometri adalah barisan suku pertama barisan geometri. Sementara deret geometri tak hingga adalah hasil penjumlahan bilangan dengan rasio yang besarnya menuju tidak terhingga.

Bisa juga diartikan bahwa deret geometri tak hingga merupakan penjumlahan suku-suku barisan geometri hingga suku ke-n yang mana n → ∞. Deret geometri tidak hingga bisa dibedakan menjadi dua jenis yakni deret geometri tidak hingga konvergen dan juga divergen.

Rumus Mencari Rasio (r)

Rasio adalah nilai perbandingan dari barisan geometri antara dua suku berurutan. Rasio dinotasikan dengan r yang dinyatakan dengan:

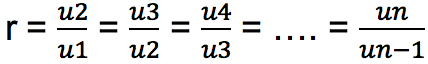
Rumus Mencari Suku ke-n (Un)

Apabila u₁, u₂, u₃, …, u_n adalah susunan dari suku-suku deret barisan geometri yang mana nilai u₁ = a serta r merupakan rasio. Sehingga suku ke-n dapat dinyatakan dengan persamaan di bawah ini:

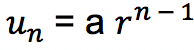
dengan n merupakan bilangan asli dimulai dari 1, 2, 3, dan seterusnya

Rumus Mencari Sn

Deret geometri tak hingga dapat dinotasikan dengan S_∞. Sehingga secara matematis deret geometri tak hingga S_∞ dapat dirumuskan dengan persamaan berikut:

S_∞ = U₁ + U₂ + U₃ + … + U_n

Rumus untuk mencari deret geometri atau penjumlahan barisan geometri disesuaikan dengan jenis deret geometri tersebut apakah divergen dan konvergen. Berikut penjelasannya.

Deret Geometri Tak Hingga Konvergen dan Divergen

Berdasarkan nilai rasio atau pembandingnya, deret geometri tidak hingga bisa dibedakan menjadi dua jenis yakni deret geometri tak hingga konvergen dan divergen.

1. Deret Geometri Tak Hingga Konvergen

Konvergen memiliki arti tidak menyebar atau memusat. Arti dari deret geometri tak hingga bersifat konvergen adalah deret barisan geometri yang mempunyai batasan atau limit jumlah. Suatu deret geometri dikatakan tak hingga konvergen bergantung kepada nilai rasionya.

Rasio yang berlaku untuk deret geometri tak hingga konvergen adalah di antara -1 dan 1, yakni -1 < r < 1 atau bisa juga dituliskan sebagai nilai mutlak r kurang dari 1, | r | < 1 dengan nilai r ≠ 0. Sehingga berlaku pada deret geometri tak hingga konvergen persamaan berikut:

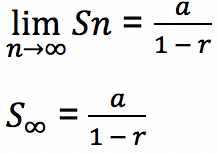
Nilai bilangan pada deret geometri tak hingga konvergen akan semakin mengecil  sehingga bisa dihitung jumlah deret geometrinya. Sebagai contoh di bawah ini adalah deret geometri tak hingga konvergen:

6 + 2 + 2/3 + 2/9 + 2/ 27 + …

Nilai barisan geometri di atas semakin lama semakin mengecil sehingga ujungnya akan semakin mendekati 0, namun tidak sama dengan 0. Untuk menghitung jumlah deret bilangan geometri di atas menggunakan rumus berikut:

a = U1 = 6

r = U2/U1 = 2/6 = 1/3

Rasio barisan geometri di atas adalah 1/3 yang terletak di antara -1 sampai 1 (-1 < r < 1). Oleh karena  itu deret geometri tak hingga di atas adalah deret geometri tak hingga konvergen karena rasio terletak antara antara -1 dan 1. Berikut rumus menghitung deret geometrinya:

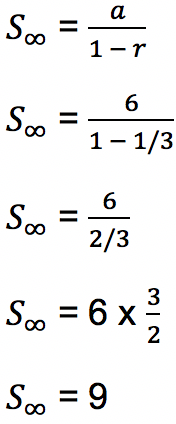
2. Deret Geometri Tak Hingga Divergen

Deret geometri divergen adalah kebalikan dari deret geometri tak hingga konvergen. Divergen bermakna menyebar sehingga deret geometri tak hingga jenis divergen adalah deret barisan geometri yang tidak terbatas jumlahnya.

Nilai rasio dikatakan sebagai deret geometri tak hingga divergen apabila r < -1 atau r > 1. Untuk deret geometri tak hingga divergen maka jumlahnya dirumuskan seperti di bawah ini:

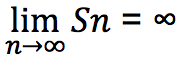
Jumlah deret geometri tak hingga divergen nilainya tidak terhingga karena nilai pada bilangannya semakin membesar serta tidak bisa dihitung jumlahnya. Sebagai contoh barisan deret geometri dibawah ini:

2 + 6 + 18 + 54 + …

Jumlah seluruhnya tidak bisa dihitung dikarenakan nilai bilangan barisan geometrinya semakin membesar.

Contoh Soal Deret Geometri Tak Hingga & Pembahasan

• Soal 1

Diketahui suatu deret geometri tak hingga suku ke 2 dan suku ke 5 berturut-turut adalah 2 dan ¼. Apabila rasio deret geometri tak hingga tersebut positif, tentukan jumlah dari seluruh suku deret geometri tak hingga tersebut.

Pembahasan

Untuk mengerjakan penjumlahan deret geometri tak hingga di atas, pertama-tama harus ditentukan terlebih dahulu besar rasionya. Karena yang diketahui adalah nilai baris geometri U2 dan U5. maka rasio deret geometri menggunakan rumus di bawah ini:

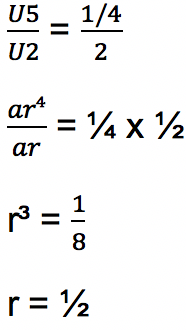
Nilai rasio ½ artinya r terletak di antara -1 dan 1 sehingga termasuk deret geometri konvergen. Maka rumus menentukan deret geometri tak hingga menggunakan rumus konvergen. Namun sebelum menghitung deret geometri, maka ditentukan terlebih dahulu U1 atau suku pertama

U2 = a x r

2 = a x ½

a = 4

Rumus menghitung deret geometri tak hingga konvergen:

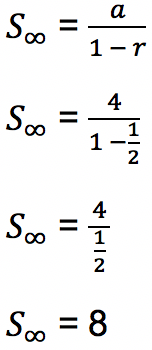
• Soal 2

Diketahui suatu deret geometri memiliki pola

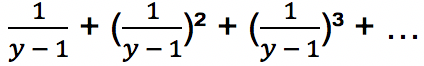
Deret geometri ini akan bernilai konvergen apabila nilai y memenuhi syarat berikut ini.

Pembahasan

Dari deret geometri

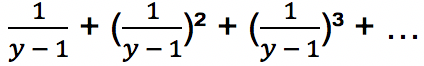
bisa dilihat bahwa rasio deret geometri tersebut adalah

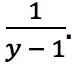
Supaya jenis deret geometri bernilai konvergen, maka nilai rasio harus berada di antara -1 dan 1 atau | r | < 1. Sehingga di bawah ini adalah cara perhitungannya.

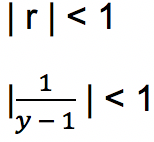
|y – 1| harus memenuhi syarat dimana y ≠ 1 karena akan membuat pecahan menjadi tidak terdefinisikan.

y – 1 > 1 atau y – 1 < -1

y > 2 atau y < 0

Sehingga nilai y yang memenuhi agar deret geometri tak hingga di atas menjadi konvergen adalah y > 2 atau y < 0.

• Soal 3

Tentukan berapa deret geometri 3 + 6 + 12 + 24 + …

Deret geometri tak hingga merupakan pejumlahan dari seluruh suku pada barisan geometri hingga tidak terhingga jumlahnya. Total penjumlahan suku barisan geometri ini ditentukan oleh jenis deret geometri apakah konvergen atau divergen. Untuk barisan geometri divergen maka jumlah deretnya tidak terhingga.