Di kehidupan sehari-hari, istilah perbandingan tentu sudah sering ditemui. Sebagai contoh perbandingan banyak digunakan untuk membandingkan jumlah siswa laki-laki dengan siswa perempuan di suatu sekolah. Oleh karena itu perbandingan adalah materi dalam Matematika yang penting untuk dipelajari.
Pengertian Perbandingan
Perbandingan sangat erat kaitannya dengan pecahan dan pembagian karena bilangan pecahan sendiri adalah notasi dari perbandingan. Perbandingan adalah pernyataan bagian dari kumpulan ataupun jumlah tertentu. Perbandingan ditulis menggunakan notasi pecahan yang sangat sederhana.
Sebagaimana pada operasi pecahan, penulisan perbandingan juga dapat disederhanakan dengan cara membagi bilangan penyebut dan pembilang menggunakan bilangan yang sama hingga bilangan tidak dapat dibagi lagi.
Perbandingan dalam Kehidupan Sehari-Hari
Konsep mengenai perbandingan berlaku dalam kehidupan sehari-hari. Perbandingan digunakan untuk menghitung berapa banyak bahan mentah yang dibutuhkan untuk membuat adonan kue apabila jumlah kue yang diproduksi ingin ditingkatkan.
Perbandingan juga bisa ditemukan penggunaannya pada penulisan skala di peta dan juga maket bangunan. Mengingat konsep perbandingan sangat erat kaitannya dengan pembagian dan pecahan, maka penting untuk memahami kedua konsep ini agar perhitungan perbandingan memberikan hasil yang tepat.
Perbandingan Senilai
Perbandingan senilai adalah perbandingan dengan dua atau lebih satuan yang mana ketika salah satu nilainya membesar maka nilai lain yang terkait juga akan ikut membesar. Begitu pula sebaliknya tatkala salah satu nilai mengecil maka nilai yang lain pun akan ikut mengecil.
Contoh perbandingan senilai adalah waktu tempuh terhadap jarak tempuh kendaraan. Ketika waktu yang ditempuh semakin lama, maka jarak tempuhnya tentu semakin jauh.
Jumlah tepung yang dibutuhkan untuk membuat kue dengan kue yang dihasilkan. Saat jumlah tepung yang digunakan semakin banyak, maka kue yang dihasilkan juga semakin banyak.
Perbandingan Berbalik Nilai
Perbandingan berbalik nilai merupakan perbandingan dua maupun lebih satuan yang mana ketika salah satu nilainya meningkat maka nilai lain yang terkait justru menurun. Sebaliknya ketika salah satu nilai menurun, maka nilai lain yang terkait justru meningkat.
Beberapa contoh kasus perbandingan berbalik nilai pada kehidupan sehari-hari adalah perbandingan antara waktu selesainya pekerjaan dengan jumlah orang yang mengerjakan. Saat jumlah pekerja semakin banyak, maka waktu selesainya pekerjaan justru semakin singkat.
Perbandingan Bertingkat
Perbandingan bertingkat adalah perbandingan bilangan yang melibatkan lebih dari satu perbandingan. Apabila pada perbandingan biasa hanya melibatkan dua variabel saja, maka pada perbandingan bertingkat melibatkan lebih dari dua variabel.
Sebagai contoh perbandingan bertingkat yakni perbandingan jumlah uang Budi dan Ani adalah 5 : 6 sementara perbandingan uang Ani dan Dodi adalah 7 : 3. Untuk menghitung perbandingan bertingkat harus dibuat rasio perbandingan uang ketiga orang tersebut.
Cara Menghitung Perbandingan
Untuk menghitung perbandingan bisa melakukan beberapa langkah berikut ini:
- Pertama-tama permasalahan yang ingin diselesaikan dibuat model terlebih dulu
- Menentukan permasalahan tersebut termasuk jenis perbandingan yang mana, apakah senilai, berbalik nilai atau bertingkat
- Menyusun persamaan perbandingan dan menghitung variabel yang ingin dicari
Rumus Perbandingan
- Rumus Perbandingan Senilai
Apabila h1 dan g1 adalah kondisi pertama dan h2 serta g2 merupakan kondisi kedua, maka rumus perbandingan senilainya menjadi:
h1 : g1 = h2 : g2
atau jika ditulis ke dalam bentuk pecahan menjadi:
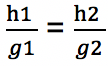
Apabila dikali silang, maka menghasilkan persamaan berikut:
h1 x g2 = h2 x g1
- Rumus Perbandingan Berbalik Nilai
Jika r1 dan p1 adalah kondisi pertama dan r2 serta p2 merupakan kondisi kedua, maka rumus perbandingan berbalik nilai menjadi:
r1 : r2 = p2 : p1
Terlihat pada persamaan di atas, posisi perbandingan di sisi kanan dan sisi kiri terbalik sehingga disebut berbalik nilai. Jika ditulis ke dalam bentuk pecahan menjadi:
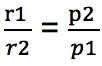
Apabila dikali silang, maka menghasilkan persamaan berikut:
r1 x p1 = r2 x p2
Contoh Soal Perbandingan
- Soal 1
Usia ayah dibandingkan usia adik adalah 9 banding 2. Jumlah usia ayah dan usia adik adalah 44 tahun. Tentukan berapakah usia adik dan ayah masing-masing?
Diketahui:
Perbandingan Usia ayah : usia adik = 9 : 2
Total usia keduanya (T) = 44 tahun
Jawab:

- Soal 2
Di sudut kota terdapat tanah kosong yang akan dibangun sebuah ruko di atasnya. Perbandingan antara luas bangunan yang akan dibangun terhadap luas tanah adalah 2 : 5. Apabila luas bangunan ruko yang akan dibangun tersebut sebesar 180 m². Tentukan berapakah luas tanah dalam m².
Diketahui:
luas bangunan yang akan dibangun : luas tanah = 2 : 5
Luas bangunan = 180 m²
Ditanya:
Luas tanah (m²)?
Jawab:

Sehingga luas tanah tempat akan dibangunnya ruko adalah 450 m²
- Soal 3
Tiga orang pelajar bisa membawa sebanyak 18 buku. Tentukan berapa banyak buku yang bisa dibawa oleh 9 orang pelajar?
Jawab:
Berdasarkan soal di atas, bisa dilihat bahwa perbandingan tersebut merupakan perbandingan senilai karena semakin banyak orang yang membawa buku, maka semakin banyak pula buku yang bisa dibawa. Sehingga rumus yang digunakan adalah rumus perbandingan senilai:

Sehingga banyak buku yang bisa dibawa oleh 9 orang pelajar sebanyak 54 buku.
- Soal 4
Diketahui seorang peternak ayam memiliki sebanyak 120 ekor ayam petelur. Tiga karung berisi pakan ternak ayam dapat habis dalam waktu satu hari. Tentukan berapa banyak pakan ternak tersebut habis apabila jumlah ayam yang dimiliki 60 ekor.
Jawab:
Bisa dilihat pada persoalan di atas bahwa persoalan tersebut termasuk perbandingan berbalik nilai. Hal ini karena semakin sedikit jumlah ayam yang dipelihara, maka semakin lama pakan ternak tersebut habis. Sehingga digunakan rumus berbalik nilai:

Sehingga pakan ternak tersebut akan habis selama 2 hari apabila jumlah ayam menjadi 60 ekor.
Kesimpulan
Perbandingan adalah pernyataan bagian dari kumpulan atau jumlah bilangan tertentu. Dalam penulisannya, perbandingan harus ditulis menggunakan pecahan yang sangat sederhana dengan cara membagi bilangan penyebut dan pembilang menggunakan bilangan yang sama.
