Logaritma: Pengertian, Sifat, Rumus, Contoh Soal

Materi logaritma berkaitan sangat erat dengan materi eksponen atau bilangan berpangkat. Logaritma adalah kebalikan dari materi bilangan berpangkat (eksponensial) yang mana pada materi eksponensial mencari hasil dari bilangan berpangkat sementara logaritma mencari besar pangkatnya. 

Pengertian Logaritma

Materi logaritma dikembangkan oleh ahli Matematika berkebangsaan Inggris, yakni John Napier yang menjelaskan terkait metode logaritma di dalam buku yang ditulis di tahun 1614 berjudul Mirifici Logarithmorum Canonis Descriptio.

Logaritma diambil dari Bahasa Latin Tengah yakni “logaritmus” yang bermakna rasio bilangan. Selain itu logaritma juga diambil dari Bahasa Yunani yakni logos dan arithmos. Logos artinya rasio dan proporsi sementara arithmos adalah bilangan.

Logaritma merupakan invers atau kebalikan dari eksponen. Cara penulisan logaritma yakni “log”. Definisi dari logaritma yakni ^alog b = c jika dan hanya jika a^c = b yang mana nilai a dan b termasuk bilangan real dengan a > 0, a ≠ 1, b > 0 serta c adalah bilangan rasional.  

Keterangan:

a = basis dengan ketentuan 0 < a < 1 atau a > 1
b = numerus, dengan ketentuan b > 0
c = hasil logaritma

Logaritma dalam Kehidupan Sehari-Hari

Pemanfaatan logaritma sangat luas dalam kehidupan sehari-hari, salah satunya digunakan dalam rumus perhitungan skala bunyi dalam satuan decibel. Untuk menghitung skala bunyi, Alexander Graham Bell merumuskan persamaan D = 10 log I/Io, dengan D merupakan skala decibel bunyi.

I merupakan intensitas bunyi dalam satuan Watt/meter² dan Io adalah intensitas bunyi paling rendah yang bisa didengar oleh telinga orang yang sehat yakni sebesar 1,0 x 10ˉ¹². Lambang log adalah notasi untuk logaritma yang memudahkan seseorang untuk menghitung intensitas bunyi dengan rentang sangat besar.

Logaritma juga bisa digunakan dalam ilmu ekonomi untuk menghitung besarnya inflasi terhadap harga barang-barang komoditas dengan kenaikan yang tetap.

Rumus Logaritma

^alog b = c sama dengan a^c = b, sehingga beberapa bilangan eksponen di bawah ini bisa diubah menjadi logaritma sebagai berikut:

• 2^x = 5
  x = ²log 5

• 4^y = 8
  y = ⁴log 8

• 6^z = 36
  z = ⁶log 36

Ada beberapa catatan terkait penulisan logaritma sebagai berikut:

• Apabila logaritma memiliki basis e (e merupakan bilangan Euler yang mana e ≈ 2,718) maka ^elog b ditulis sebagai ln b.
• Bilangan basis atau pokok 10 tidak perlu ditulis, sehingga untuk bilangan ¹⁰log b ditulis log b saja.

Sifat Logaritma

Logaritma mempunyai beberapa sifat dasar yang ditarik dari definisi logaritma yang merupakan kebalikan dari perpangkatan. Berikut sifat logaritma:

1. Apabila a dan b merupakan bilangan real, yang mana bilangan a > 0 dan a ≠ 1, sehingga berlaku padanya:

^alog a = 1
^alog 1 = 0
^alog aⁿ = n

2. Pada persamaan logaritma ^alog (b x c) = ^alog b + ^alog c, dengan syarat bilangan a, b dan c adalah bilangan real positif, yang mana nilai a ≠ 1 dengan nilai b > 0. Sifat ini dibuktikan melalui cara berikut:

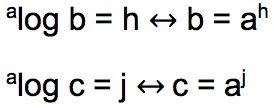
Selanjutnya dikalikan nilai b dan juga c, sehingga menghasilkan:

b x c = a^h x a^j
b x c = a^{h + j
a}log (b x c) = h + j (Substitusi h dan j)
^alog (b x c) = ^alog b + ^alog c

3. Pada persamaan logaritma berlaku ^alog (c/d) = ^alog c – ^alog d, dengan syarat bilangan a, c dan d adalah bilangan real positif, yang mana nilai a ≠ 1 dengan nilai c > 0.

4. Pada persamaan logaritma berlaku ^alog cⁿ = n ^alog c, dengan syarat bilangan a, c dan n adalah bilangan asli, yang mana nilai a > 0, c > 0, dan a ≠ 1

5. Pada persamaan logaritma berlaku ^alog b = ^clog b/ ^clog a = 1/^blog a, dengan syarat bilangan a, b dan c adalah bilangan real positif, yang mana nilai a, b dan c ≠ 1.

6. Pada persamaan logaritma berlaku ^{a^m}log cⁿ = n/m (^alog c), dengan syarat bilangan a dan c adalah bilangan real positif, yang mana nilai a ≠ 1, m dan n bilangan rasional serta m ≠ 0.

7. Pada persamaan logaritma berlaku a^{a log b} = b, dengan syarat bilangan a dan b adalah bilangan real positif, yang mana nilai a ≠ 1.

8. Pada persamaan logaritma berlaku ^alog (c/d) = – ^alog (d/c)

Persamaan Logaritma

Persamaan logaritma merupakan persamaan yang mempunyai dua bentuk logaritma di sisi kiri dan kanan yang dipisahkan oleh tanda sama dengan “=” yang mana variabelnya terdapat dalam numerus atau basis. Berikut adalah contoh dari persamaan logaritma:

ᵃlog h(x) = ᵃlog n

ᵃlog h(x) = ᵃlog g(x)

ᵃlog h(x) = ^blog h(x)

h(x) log g(x) = h(x) log f(x)

h(x) log g(x) = f(x) log g(x)

A (ᵃlog h(x)) 2 + B (ᵃlog h(x)) + C = 0

Pertidaksamaan Logaritma

Pertidaksamaan logaritma merupakan bentuk logaritma di sisi kiri dan kanan yang memiliki nilai berbeda, misal lebih besar dari (>) dan lebih kecil dari (<).

ᵃlog h(x) < ᵃlog g(x), apabila a > 0 maka h(x) < g(x)

ᵃlog h(x) > ᵃlog g(x), apabila a > 0 maka h(x) > g(x)

Contoh Soal Logaritma

1. Tentukan nilai dari persamaan logaritma berikut ini:

a. ³log 729
b. ⁴log 256

2. Tentukan nilai y dari persamaan berikut ini: log² y + log y = 6, yang mana log² y merupakan notasi untuk (log y)².

3. Tentukan nilai x dari log 1000.000 = x

Baca Juga : Kumpulan Contoh Soal Logaritma

Kesimpulan

Oleh karena sifat materi logaritma yang berkebalikan dengan materi bilangan berpangkat atau eksponensial, maka untuk dapat menguasai logaritma juga harus menguasai materi eksponensial. Logaritma adalah cabang di Matematika yang digunakan untuk mencari besar pangkat bilangan tertentu.