Salah satu materi penting yang akan dipelajari di bangku kelas XII SMA adalah matrik dan cara perkalian matriks. Materi matriks sendiri sangat berguna dalam dunia pemrograman komputer maupun untuk memudahkan penyelesaian berbagai persoalan di kehidupan sehari-hari.
Pengertian Matriks
Matrik merupakan susunan simbol, bilangan ataupun karakter yang disusun dengan menggunakan susunan baris dan kolom seperti pada bangun persegi. Simbol, bilangan serta karakter yang ada di dalam matriks disebut sebagai elemen matriks.
Penulisan matriks dinotasikan menggunakan huruf capital, misalnya matriks A dan matriks B. Sementara elemen matrik berupa huruf atau karakter menggunakan huruf kecil. Di dalam matriks terdapat ordo yang merupakan bilangan untuk menunjukkan jumlah baris serta kolom matriks.
Pembacaan ordo adalah baris x kolom. Sebagai contoh, di bawah ini merupakan matriks A2 x 2

Matriks A memiliki baris berjumlah 2 dan kolom berjumlah 2 dengan elemen matriks terdiri dari 1, 5, 2 dan 6.
Cara Perkalian Matriks
Operasi hitung pada matriks melibatkan penjumlahan, pengurangan dan juga perkalian. Perkalian matriks merupakan perkalian dari elemen-elemen di dalam matriks yakni dikalikannya elemen baris dengan elemen setiap kolom matriks lainnya yang mempunyai jumlah baris sama.
Oleh karena itu jumlah baris dan kolom matriks menjadi syarat perkalian matriks. Misalnya agar dapat dilakukan perkalian antara matriks A dan matriks B maka diharuskan jumlah kolom matriks pertama sama banyaknya dengan baris pada matriks kedua.
Hasil perkalian dari matriks A dan matriks B ini berupa matriks yang memiliki jumlah baris sama dengan matriks pertama dan jumlah kolom sama dengan matriks kedua. Simak ilustrasi hasil perkalian matriks di bawah ini.
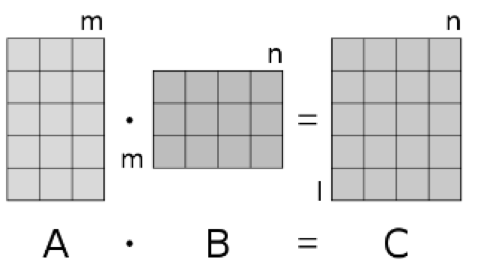
Misalnya perkalian matriks Ag x h x Bh x i = Cg x i
Sifat Perkalian Matriks
Perkalian matriks mempunyai beberapa sifat yang menjadi karakteristik dan rumus penting perkalian matriks:
- Perkalian dengan matriks nol:
B x 0 = 0 x B = 0
- Sifat perkalian asosiatif
Sifat perkalian asosiatif yakni perkalian antara tiga matriks atau lebih yang mana hasil perkalian akan sama tidak bergantung kepada urutan perkalian, selama syarat jumlah baris dan kolom perkalian matriks terpenuhi.
(H x I) x J = H x (I x J)
- Sifat Distributif Kiri dan Kanan
H x (I + J) = H x I + H x J
(H + I) x J = H x J + I x J
- Sifat Perkalian Matriks dengan Konstanta a
a (H x I) = (a x H) x I = H x (a x I)
- Sifat Perkalian Matriks dengan Matriks Identitas
H x I = I x H = H
Kumpulan Contoh Soal Perkalian Matriks Dan Pembahasannya
- Soal 1
Diketahui terdapat matriks
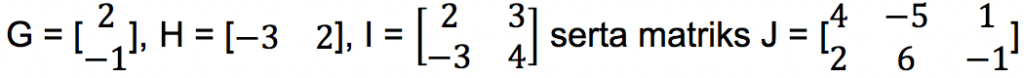
Tentukan nilai dari perkalian matriks berikut ini:
a. G x H
b. H x I
c. I x J
d. G x I
Jawab:
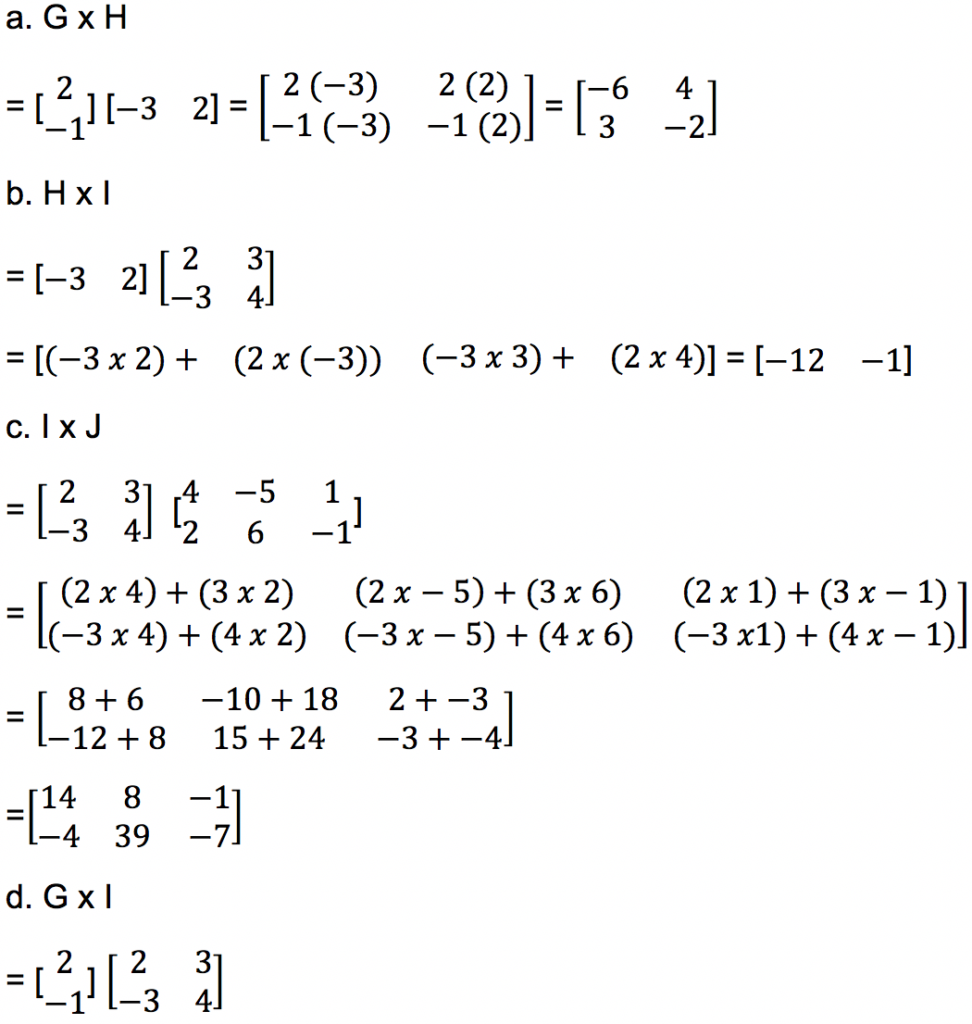
Tidak bisa dioperasikan perkalian karena jumlah kolom dari matriks G tidak sama jumlahnya dengan jumlah baris dari matriks I
- Soal 2
Hitunglah hasil perkalian dari dua matriks berikut ini:
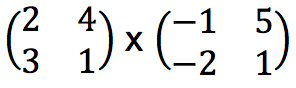
Jawab:

- Soal 3
Tentukan berapakah nilai a + b yang memenuhi perkalian matriks di bawah ini:
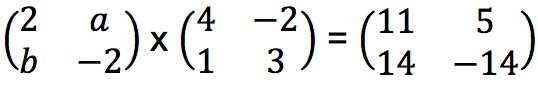
Jawab:
Cara untuk menyelesaikan soal di atas adalah dengan mengalikan kedua matriks kemudian membandingkan hasil perkalian tersebut dengan hasil perkalian matriks yang sudah disediakan di soal.
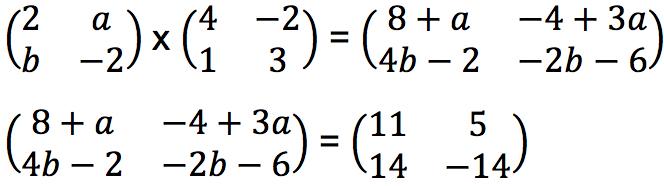
Selanjutnya dapat disamakan nilai setiap elemennya terhadap posisi elemen matriks sehingga diperoleh:
8 + a = 11
a = 11 – 8 = 3
4b – 2 = 14
4b = 14 + 2
4b = 16
b = 4
Pemilihan elemen yang ingin digunakan untuk mencari nilai variabel dibebaskan selama posisinya bersesuaian.
Sehingga:
a + b
= 3 + 4
= 7
- Soal 4
Tentukan berapakah nilai x – y yang memenuhi perkalian matriks di bawah ini:
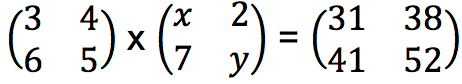
Jawab:
Seperti pada nomor 3, cara untuk menyelesaikan soal di atas adalah dengan mengalikan kedua matriks kemudian membandingkan hasil perkalian tersebut dengan hasil perkalian matriks yang sudah diberikan pada soal.
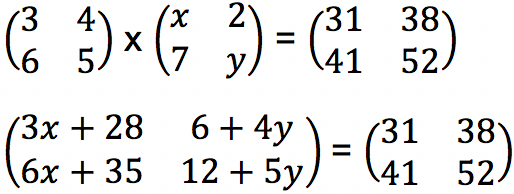
Selanjutnya dapat disamakan nilai setiap elemennya terhadap posisi elemen matriks sehingga diperoleh:
6 + 4y = 38
4y = 38 – 6
4y = 32
y = 8
6x + 35 = 41
6x = 41 – 35
6x = 6
x = 1
Sehingga nilai dari x – y adalah
= 1 – 8
= -7
- Soal 5
Diketahui matriks
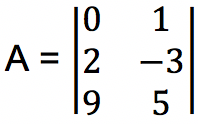
tentukan nilai dari di bawah ini:
a. 4A
b. 5A
c. 2 (3A)
Jawab:

- Soal 6
Jika diketahui matriks-matrik di bawah ini:
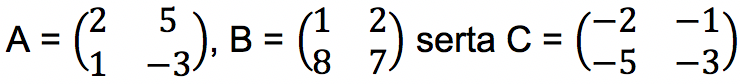
Tentukan berapakah nilai dari AB dan A (B + C)
Jawab:
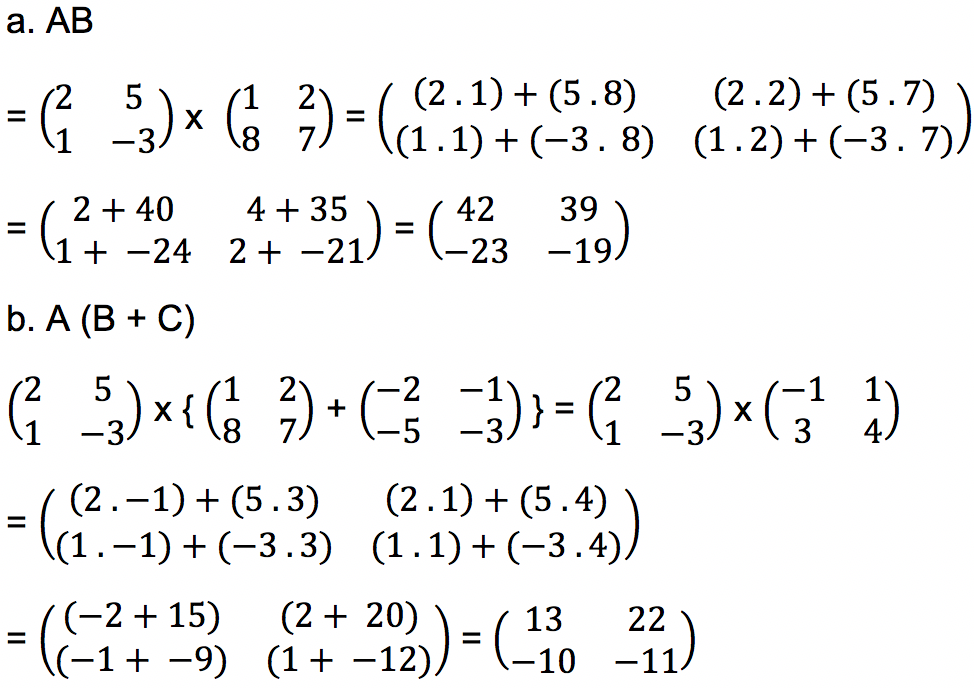
Baca Juga : Kumpulan Contoh Soal Matriks & Pembahasannya
Cara perkalian matriks dilakukan dengan mengalikan elemen-elemen di dalam matriks yakni elemen baris matriks di depan atau pertama dengan elemen setiap kolom matriks di belakang atau kedua yang mempunyai jumlah baris sama. Untuk memudahkan perhitungan harus dipahami sifat perkalian matriks.
