Integral merupakan salah satu materi dalam Matematika yang erat kaitannya dengan materi turunan atau diferensial. Oleh karena itu, sebelum memahami konsep integral, sebaiknya pelajar sudah memahami materi diferensial atau turunan yang sangat berguna dalam memahami penyelesaian operasi integral.
Definisi Integral
Sebenarnya jika dilihat dari sejarah, operasi hitung integral ditemukan terlebih dulu baru selanjutnya ditemukan konsep turunan atau diferensial. Namun, pemahaman pelajar mengenai konsep integral akan lebih mendalam apabila sudah memahami konsep turunan atau diferensial suatu fungsi.
Materi integral sendiri adalah invers atau kebalikan dari materi diferensial atau turunan. Sebagai contoh apabila turunan dari fungsi f (x) = x² + 10 adalah f’ (x) = 2x, maka fungsi yang turunannya adalah f’ (x) = 2x disebut sebagai pengintegralan atau antiturunan.
Fungsi F (x) disebut sebagai antiturunan atau integral dari f (x) pada suatu domain apabila
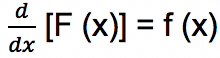
Contoh Penerapan Integral
Salah satu penerapan utama dari konsep integral dalam Matematika dan ilmu hitung adalah untuk menghitung luas suatu bidang datar ataupun luas kurva. Tidak semua bangun datar diketahui rumus luasnya.
Bangun datar dengan bentuk tidak beraturan tidak mempunyai rumus yang pasti seperti bangun datar beraturan. Oleh karena itu dibutuhkan konsep integral untuk menghitung luas bangun datar tidak beraturan. Hal ini juga terkait dengan pengertian integral tertentu sebagai luas suatu bidang datar.
Rumus Integral
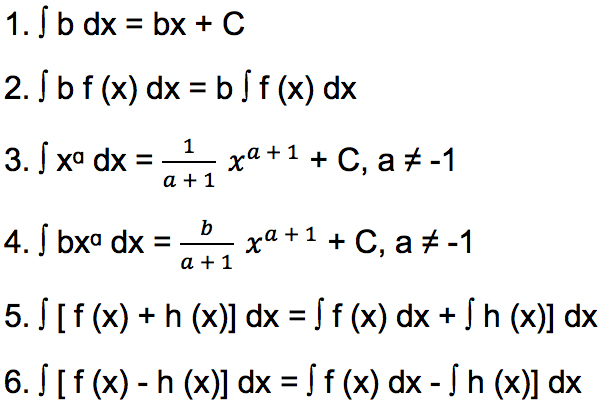
Pelajari Juga Turunan
Integral Tak Tentu
Integral tak tentu disebut sebagai anti turunan oleh Leibniz. Sehingga proses dalam menghitung anti turunan disebut sebagai mengintegralkan. Untuk menuliskan integral tak tentu maka dinotasikan dengan simbol
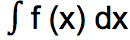

Dimisalkan ada fungsi sebagai berikut:
y1 = x² + 2x – 5
y2 = x² + 2x + 5
Kedua fungsi di atas mempunyai turunan yang sama yakni
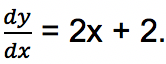
Apabila turunan
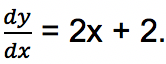
dicari nilai integralnya, maka bisa didapatkan berbagai fungsi seperti:
y = x² + 2x – 3
y = x² + 2x + 2
y = x² + 2x – 10 dan seterusnya.
Sehingga bisa disimpulkan bahwa integral fungsi turunan di atas bisa menghasilkan berbagai kemungkinan fungsi. Perbedaan dari setiap fungsi terdapat pada bilangan tetapnya atau konstantanya seperti angka -3, 2, -10 dan lainnya.
Bilangan ini dinotasikan dengan C. Keberadaan C sebagai hasil integral ini disebut integral tak tentu.
Notasi integral tak tentu dituliskan dalam bentuk berikut:
f (x) dx = F (x) + C
Keterangan:
f (x) = turunan dari fungsi F (x)
f (x) dx = notasi integral tak tentu
F (x) = fungsi dalam variabel x
C = konstanta bilangan real
Integral Tentu
Berbeda dengan integral tak tentu, integral tentu
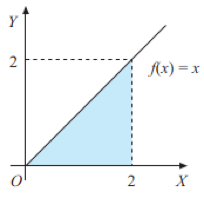
Pada Gambar 1 di atas berlaku rumus untuk menghitung luas di bawah garis lurus dengan fungsi linear f (x) adalah:
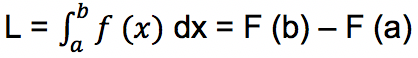
Makna persamaan di atas adalah L merupakan luas daerah yang dibatasi oleh kurva y = f (x), sumbu X, serta garis dari mulai x = a hingga garis x = b. F (x) sendiri merupakan antiturunan atau integral dari fungsi f (x) pada
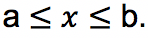
Integral Trigonometri
Persamaan trigonometri berupa sinus, cosinus dan tangen juga memiliki aturan pengintegralan.
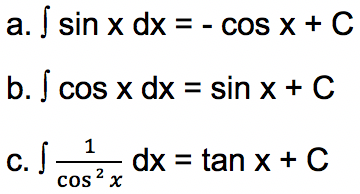
Pelajari Juga Perbandingan Trigonometri
Integral Eksponensial
Fungsi eksponensial dituliskan dengan ex. Fungsi eksponensial jika diintegralkan akan membentuk persamaan berikut:
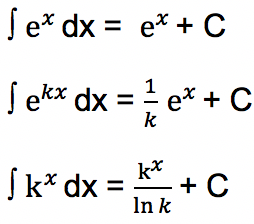
Integral Substitusi
Apabila g suatu fungsi yang bisa didiferensialkan serta r adalah bilangan rasional yang bernilai tidak sama dengan 0, maka berlaku padanya rumus integral substitusi:
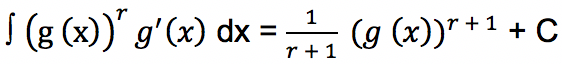
C adalah konstanta serta r ≠ -1
Integral Parsial
Apabila g dan h merupakan fungsi yang bisa didiferensialkan, sehingga aturan integral parsial yang berlaku pada fungsi tersebut sebagai berikut:
∫ g dh = g.h – ∫ h dg
Contoh Soal Integral
1. Tentukan nilai integral dari fungsi di bawah ini:
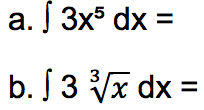
Jawab:
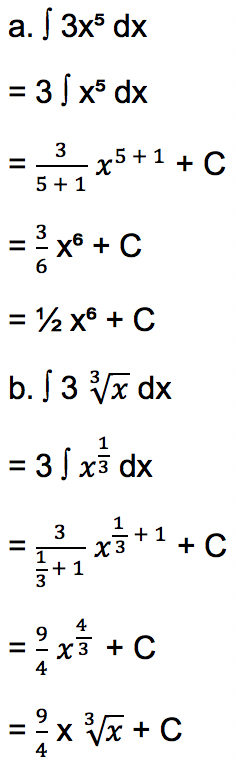
2. Diketahui nilai kemiringan garis singgung kurva pada titik (x, y) yakni 2x – 8. Apabila kurva tersebut melalui titik (3, -2). Tentukanlah persamaan kurva tersebut.
Jawab:
Untuk menghitung persamaan kurva dengan diketahui persamaan gradient garis singgung adalah dengan mengintegralkan persamaan garis singgung tersebut.
f’ (x) = dy/dx = 2x – 8
f (x) = y = ∫ (2x – 8) dx = x² – 8x + C
Kurva tersebut melalui titik (3, -2) sehingga konstanta C dapat dicari dengan substitusi nilai x dan y ke persamaan garis singgung:
f (x) = x² – 8x + C
f (3) = (3)² – 8 (3) + C
-2 = 9 – 24 + C
C = 13
Sehingga persamaan kurva adalah f (x) = x² – 8x + 13
Baca Juga : Kumpulan Contoh Soal Integral & Pembahasannya
Kesimpulan
Integral adalah invers atau kebalikan dari materi diferensial atau turunan. Agar pemahaman mengenai materi integral lebih utuh, maka dibutuhkan pemahaman yang mendalam terkait materi turunan. Integral bermanfaat dalam berbagai bidang kehidupan seperti perhitungan luas kurva dan volume benda putar.
