Kesebangunan dan Kekongruenan: Definisi, Ilustrasi, Soal

Materi kesebangunan dan kekongruenan mulai diajarkan pada SMP kelas 9 yang membahas mengenai konsep kesebangunan pada bangun datar serta penggunaan konsep ini dalam memecahkan masalah. Dengan memahami konsep ini, maka bisa diidentifikasi bangun datar yang kongruen dan sebangun.

Definisi Kesebangunan dan Kekongruenan

Materi kesebangunan dan kekongruenan sangat bergantung kepada konsep perbandingan yang sudah dipelajari di SMP kelas 7. Konsep perbandingan nantinya digunakan untuk membandingkan antara sisi-sisi pada beberapa bangun datar.

Dua bangun datar dapat dikatakan memiliki kesebangunan apabila masing-masing sisi yang bersesuaian pada bangun datar tersebut mempunyai perbandingan yang sama serta sudut-sudut yang bersesuaian sama besar. Konsep kesebangunan berlaku untuk berbagai jenis bangun datar.

Syarat dua buah bangun datar disebut sebangun adalah apabila memenuhi dua persyaratan berikut ini:

• Sudut-sudut yang bersesuaian dari kedua bangun segitiga sama besar
• Panjang sisi yang bersesuaian dari kedua bangun segitiga mempunyai perbandingan yang senilai

Bangun datar yang memiliki kesebangunan dapat dilambangkan dengan notasi ≈.

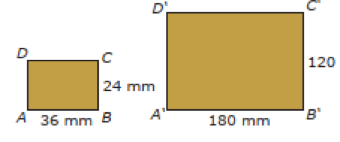
Contoh bangun persegi panjang yang saling sebangun tampak di Gambar 1. di atas pada bangun persegi panjang ABCD dan persegi panjang A’B’C’D’. Bisa dilihat pada Gambar 1. pasangan sisi-sisi yang saling bersesuaian memiliki perbandingan nilai yang sama, dimana:

• Sisi AB : sisi A’B’ = 36 : 180 = 1 : 5
• Sisi BC : sisi B’C’ = 24 : 120 = 1 : 5
• Sisi AD : sisi A’D’ = 24 : 120 = 1 : 5
• Sisi CD : sisi C’D’ = 36 : 180 = 1 : 5

Dapat dilihat pada perbandingan di atas bahwa sisi-sisi yang bersesuaian mempunyai perbandingan sebanding atau senilai. Perbandingan sisi yang saling bersesuaian pada kedua persegi panjang ditunjukkan pada persamaan berikut ini:

AB/A’B’ = BC/B’C’ = AD/A’D’ = CD/C’D’ = 1/5

Seperti yang diketahui bahwa besar masing-masing sudut bangun persegi panjang adalah siku-siku (90⁰) sehingga seluruh sudut yang bersesuaian pada bangun persegi panjang besarnya sama.

Konsep kekongruenan pada bangun datar berbicara mengenai dua buah bangun datar yang mempunyai sisi bersesuaian sama panjang dan juga sudut yang bersesuaian sama besar. Sehingga, dua buah benda bisa dikatakan kongruen hanya apabila kedua benda tersebut mempunyai ukuran dan bentuk yang sama.

Kesebangunan & Kekongruenan dalam Kehidupan Sehari-Hari

Konsep kesebangunan dan kekongruenan banyak dimanfaatkan untuk melakukan pengukuran terhadap suatu objek yang ada di kehidupan sehari-hari. Sebagai contoh, konsep ini bisa digunakan untuk mengukur lebar suatu kali atau sungai yang besar.

Mengukur lebar kali atau sungai yang sangat besar tentu sulit jika dilakukan secara manual menggunakan alat pengukur, sehingga pengukuran bisa dilakukan secara tidak langsung. Caranya dengan menggunakan konsep kesebangunan dan kekongruenan bangun segitiga.

Cukup membuat dua segitiga yang mana segitiga besar memiliki alas berupa lebar sungai ditambah alas dari segitiga yang lebih kecil di pinggir sungai.

Kesebangunan

1. Kesebangunan Segitiga

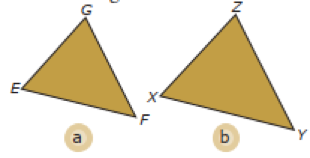
Seperti yang dijelaskan di atas, bangun yang saling sebangun mempunyai sisi bersesuaian sebanding dengan sudut-sudut bersesuaian yang sama besar. Pada Gambar 2. di atas, masing-masing segitiga yang sebangun berlaku persamaan berikut ini:

EF/XY = EG/XZ = FG/YZ

dimana besar sudut F = sudut Y, sudut G = sudut Z, dan sudut E = sudut X.

Umumnya soal mengenai kesebangunan segitiga hadir dalam bentuk dua buah segitiga yang saling bertumpuk seperti pada Gambar 3. di bawah ini.

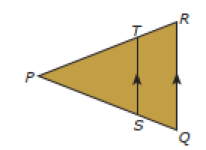
Cara pengerjaan soal kesebangunan segitiga pada segitiga yang saling bertumpuk sebenarnya sama dengan persamaan kesebangunan bidang segitiga di Gambar 2. Berikut adalah hubungan yang dihasilkan dari kesebangunan segitiga PST dan PQR.

PT/PR = PS/PQ = ST/QR

Sudut PTS = sudut PRQ, sudut TPS = sudut RPQ, sudut PST = sudut PQR

2. Kesebangunan Trapesium

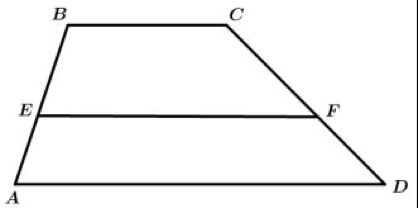
Konsep kesebangunan juga banyak diterapkan pada bangun datar trapesium baik itu trapesium siku-siku, trapesium sembarang dan trapesium sama kaki. Pada Gambar 4. di atas terdapat dua trapesium yang sebangun yakni trapesium ADCB dan trapesium EFCB.

Pada trapesium tersebut berlaku:

• Sudut yang bersesuaian sama besar yakni sudut BCD = sudut BCF, sudut ABC = EBC, sudut DAB = sudut FEB, sudut CDA = sudut CFE.
• Sisi-sisi pada kedua trapesium di atas juga mempunyai perbandingan yang sama yakni sisi CD = sisi CF, sisi AB = sisi EB, sisi AD = sisi EF.
• Perbandingan kedua trapesium dituliskan sebagai berikut: AB/EB = AD/EF = CD/CF

Kekongruenan

Untuk lebih memahami konsep kekongruenan pada bangun datar, amati Gambar 2. di bawah ini. Gambar 2 menunjukkan dua buah bangun datar persegi panjang ABCD dan BEFC.

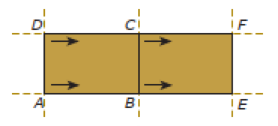
Kedua persegi panjang ABCD dan BEFC baru bisa dikatakan kongruen hanya jika panjang setiap sisi yang bersesuaian sama besar misalnya:

• sisi AB = sisi BE
• sisi BC = sisi EF
• sisi CD = sisi FC
• sisi AD = sisi BC

Selain sisi yang bersesuaian sama panjang, syarat berikutnya dua buah bangun dikatakan kongruen jika sudut-sudutnya yang bersesuaian sama besar. Sebagai contoh pada bangun persegi panjang di atas maka keempat sudutnya adalah siku-siku.

Berdasarkan pengertian konsep kongruen, bisa disimpulkan bahwa setiap bangun yang kongruen sudah pasti sebangun, namun dua bangun datar yang sebangun belum tentu dapat dikatakan kongruen.

Pelajari Juga Bangun Datar

Contoh Soal

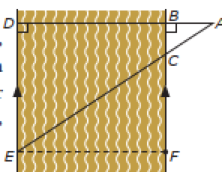
Diketahui di sebuah desa terdapat sungai yang sangat lebar dan akan dilakukan pembuatan jembatan baru dari bahan bambu. Sebelum dilakukan pembangunan harus dihitung terlebih dulu lebar sungai. Untuk menghitung lebar sungai ditandailah beberapa titik pada pinggir sungai yakni titik A, B, C, D, dan E.

Saat diukur, diketahui panjang sisi AB = 4 m, panjang DE dan BF sama-sama 12 m, dan panjang BC = 3 m. Tentukan lebar sungai tersebut.

Kesimpulan

Konsep kesebangunan dan kekongruenan sangat berkaitan dengan bangun datar yang sangat bermanfaat dalam perhitungan di kehidupan sehari-hari. Konsep kesebangunan bisa digunakan untuk menghitung lebar atau panjang suatu objek benda yang sulit dihitung menggunakan alat pengukur biasa.