Teorema Pythagoras adalah salah satu materi yang wajib dipelajari ketika membahas segitiga terutama segitiga siku-siku. Teorema Pythagoras dicetuskan oleh seorang tokoh Matematika bernama Pythagoras. Teorema ini dikeluarkan dalam rangka menemukan hubungan antara sisi-sisi pada bangun segitiga.
Definisi Pythagoras
Teorema Pythagoras merupakan teorema dalam Matematika yang membahas mengenai keterkaitan antara ketiga sisi pada bangun segitiga siku-siku. Seperti yang diketahui bahwa pada segitiga siku-siku ada dua sisi yang saling tegak lurus dan membentuk sisi siku-siku dan satu sisi di depan sudut siku-siku.
Satu sisi yang ada di depan sisi siku-siku disebut sebagai sisi miring atau hipotenusa. Hipotenusa atau sisi miring pada segitiga siku-siku merupakan sisi yang paling panjang.
Di dalam teorema Pythagoras membuktikan bahwa ternyata sisi miring tidak hanya mempunyai ukuran paling panjang namun juga ada hubungan antara ketiga sisi tersebut.
Penerapan Pythagoras
Sebagaimana cabang ilmu Matematika lainnya, mempelajari Pythagoras juga memberikan manfaat bagi kehidupan sehari-hari. Pythagoras bermanfaat dalam perhitungan bangun datar dan juga berbagai bangun ruang.
Seperti yang diketahui ada banyak aplikasi bangun datar dan juga bangun ruang di lingkungan sekitar. Rumus Pythagoras sangat bermanfaat bagi para tukang bangunan tradisional untuk membentuk sisi sebuah ruangan agar tepat siku-siku.
Caranya adalah tukang bangunan tersebut cukup menggunakan prinsip triple Pythagoras saat memasang patok-patok pondasi bangunan. Triple Pythagoras yang sering digunakan tukang bangunan tradisional adalah 3, 4 dan 5.
Tukang bangunan akan memasang dua buah patok sisi siku-siku 3 meter dan 4 meter kemudian mengukur sisi miringnya apakah tepat 5 meter atau tidak. Jika tepat terukur 5 meter dari ujung ke ujung maka artinya sudut bangunan tersebut tepat siku-siku.
Teorema Pythagoras
Teorema Pythagoras berbunyi bahwa pada segitiga siku-siku berlaku jumlah kuadrat dari dua sisi siku-siku sama dengan nilai kuadrat sisi miring.
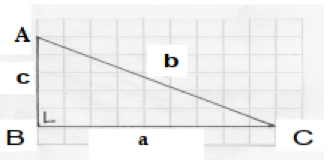
Pada Gambar 1 di atas merupakan segitiga siku-siku ABC yang mana sisi b adalah hipotenusa atau sisi miring, sisi c dan sisi a merupakan sisi pembentuk sudut siku-siku. Menurut teorema Pythagoras, kuadrat dari sisi b nilainya sama dengan jumlah kuadrat dari sisi a dan sisi c.
Rumus Pythagoras
Berdasarkan bunyi teorema Pythagoras di atas, maka hubungan antara sisi a, sisi b dan sisi c pada Gambar 1 dapat dituliskan dengan persamaan berikut:
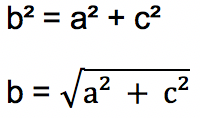
Keterangan:
a = sisi pembentuk siku-siku segitiga
b = sisi miring segitiga siku-siku (hipotenusa)
c = sisi pembentuk siku-siku segitiga
Dari rumus dasar Pythagoras di atas juga dapat diturunkan persamaan sisi-sisi segitiga siku-siku untuk menghitung sisi selain hipotenusa.
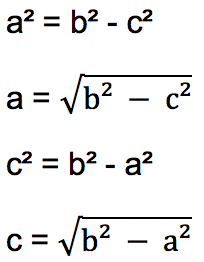
Pembuktian Teorema Pythagoras
Untuk membuktikan teorema Pythagoras, maka bayangkan jika terdapat tiga buah persegi dengan ukuran panjang tertentu. Pertama-tama, terdapat bangun persegi dengan panjang sisi AB adalah 8 kotak. Bangun persegi dengan sisi 8 kotak ini diwarnai dengan warna merah.
Bangun persegi yang kedua adalah persegi dengan panjang sisi 6 kotak yakni sisi BC yang diwarnai dengan warna biru. Selanjutnya hitung berapakah luas kedua persegi tersebut menggunakan rumus luas persegi sebagai berikut:
- Luas Persegi AB = sisi x sisi
Luas Persegi AB = 8 x 8
Luas Persegi AB = 64
- Luas Persegi BC = sisi x sisi
Luas Persegi BC = 6 x 6
Luas Persegi BC = 36
Terakhir buatlah sebuah bangun persegi yang diwarnai dengan warna kuning dan mempunyai sisi terpanjang yakni sisi AC sepanjang 10 kotak. Tentukan luas dari bangun persegi AC ini.
- Luas Persegi AC = sisi x sisi
Luas Persegi AC = 10 x 10
Luas Persegi AC = 100
Ketiga buah persegi tersebut kemudian ditempelkan saling berhimpitan hingga membentuk sebuah segitiga siku-siku ABC seperti Gambar 2 di bawah ini.
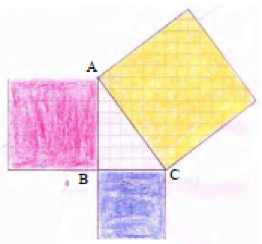
Terlihat pada Gambar 2 di atas bahwa ketika ketiga bangun persegi saling didekatkan terbentuk suatu bangun segitiga siku-siku di celah ketiga persegi. Bangun segitiga siku-siku ABC tersebut mempunyai sisi miring AC yakni sisi terpanjang dari bangun persegi terbesar.
Apabila dihitung, jumlah dua luas persegi paling kecil yakni persegi dengan sisi 6 kotak serta 8 kotak sama dengan luas persegi paling besar yakni 10 kotak.
Luas persegi AC = Luas persegi AB + Luas persegi BC
AC² = AB² + BC²
100 = 64 + 36
100 = 100
Dari percobaan di atas kemudian ditarik kesimpulan mengenai teorema Pythagoras yakni jumlah kuadrat dari dua sisi siku-siku sama dengan kuadrat dari sisi miringnya.
Tripel Pythagoras
Di dalam materi pembahasan Pythagoras terdapat satu cabang yang penting dipahami yakni konsep tripel Pythagoras. Tripel Pythagoras merupakan pasangan tiga bilangan asli yang sesuai dengan teorema Pythagoras.
Dengan mengingat bilangan mana saja yang termasuk ke dalam tripel Pythagoras maka tidak perlu lagi menghitung sisi-sisi segitiga untuk menentukan apakah bangun segitiga tersebut termasuk segitiga siku-siku atau bukan.
Beberapa pasangan bilangan yang tergolong tripel Pythagoras sebagai berikut:
a. Bilangan 3, 4, 5
b. Bilangan 6, 8, 10
c. Bilangan 5, 12, 13
d. Bilangan 7, 24, 25
e. Bilangan 8, 15, 17
f. Bilangan 9, 40, 41
Umumnya para tukang bangunan memanfaatkan bilangan tripel Pythagoras 3, 4, 5 dan bilangan 6, 8, 10 saat membuat pondasi rumah.
Contoh Soal Pythagoras
- Soal 1
Diketahui sebuah segitiga HIJ memiliki sudut siku-siku di I dengan panjang sisi HI adalah 7 cm dan panjang sisi IJ adalah 24 cm. Tentukan:
a. Sketsa dari bangun segitiga siku-siku HIJ
b. Panjang dari sisi miringnya (hipotenusa)
c. Sisi yang manakah dari bangun segitiga HIJ merupakan sisi paling panjang
Jawab:
a. Berdasarkan informasi mengenai panjang sisi-sisi siku-siku yang sudah dijelaskan di atas, bisa digambarkan sketsa bangun segitiga siku-siku berikut ini:
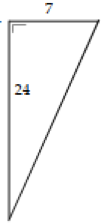
b. Sisi miring bangun segitiga HIJ adalah sisi HJ dapat dihitung menggunakan teorema Pythagoras:
HJ² = HI² + IJ²
HJ² = 7² + 24²
HJ² = 49 + 576
HJ² = 625
HJ = √625
HJ = 25 cm
c. Bisa dilihat pada panjang sisi-sisi segitiga HIJ di atas bahwa sisi terpanjangnya adalah sisi HJ atau sisi miring (hipotenusa)
- Soal 2
Diketahui segitiga sama kaki ACB seperti gambar di bawah. Tentukan berapa tinggi segitiga tersebut.
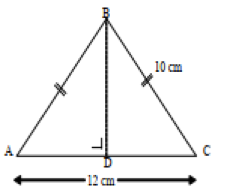
Jawab:
Untuk menghitung tinggi segitiga sama kaki bisa menggunakan teorema Pythagoras. Tinggi segitiga sama kaki membagi alas menjadi dua sama besar dan membentuk sisi siku-siku.
t² = BC² – CD²
t² = 10² – 6²
t² = 100 – 36
t = √64 = 8 cm
Memahami teorema Pythagoras dapat membantu dalam menentukan panjang setiap sisi pada segitiga siku-siku. Selain itu, teorema Pythagoras juga berguna dalam memecahkan masalah yang berkaitan dengan bangun datar.
