Fibonacci: Pengertian, Deret, Rumus, Contoh Soal

Bilangan yang ada dalam kehidupan sehari-hari apabila disusun secara teratur umumnya akan memunculkan urutan yang bersifat teratur dan tetap. Urutan bilangan yang tersusun secara teratur disebut pola. Salah satu pola bilangan dalam Matematika yang banyak dipelajari adalah bilangan Fibonacci.

Pengertian Fibonacci

Pola bilangan Fibonacci dirumuskan oleh seorang ilmuwan Matematika bernama lengkap Leonardo of Pisa. Leonardo of Pisa melakukan perjalanan ke berbagai daerah kekuasaan Khilafah Islam di Afrika Utara yakni Aljazair yang sedang dalam masa keemasannya.

Di negeri-negeri inilah Leonardo of Pisa belajar ilmu Matematika dan mengembangkan kegemarannya pada ilmu bilangan. Apalagi pada saat itu orang Eropa masih menggunakan angka Romawi yang cukup merepotkan jika digunakan dalam perhitungan Matematika.

Leonardo of Pisa bersama ayahnya selama berada di Aljazair kemudian mempelajari angka arab yang jauh lebih efisien dalam perhitungan Matematika yakni 1 – 9 serta angka 0 dari guru-guru Arab. Fibonacci pun belajar mengenai algoritma komputasi pada transaksi bisnis.

Leonardo of Pisa pun menuliskan karyanya dalam buku berjudul Liber Abaci. Di dalam buku ini ia menjelaskan teka-teki bilangan yang pada hari ini dikenal sebagai bilangan Fibonacci.

Pola bilangan Fibonacci adalah himpunan bilangan yang mana setiap suku bilangannya adalah jumlah dari dua suku yang ada di depannya. Pola bilangan Fibonacci diartikan sebagai susunan bilangan yang memiliki awalan angka 0 dan 1.

Angka selanjutnya didapatkan dengan menjumlahkan kedua bilangan sebelumnya berturut-turut.

Contoh Penerapan Fibonacci

Penerapan bilangan Fibonacci sebenarnya ada cukup banyak dalam kehidupan sehari-hari. Pola bilangan Fibonacci bisa dilihat pada susunan dari daun bunga ataupun segmen-segmen yang terdapat di dalam biji cemara atau buah nanas.

Jumlah mahkota bunga yang tersusun bisa dituliskan menggunakan salah satu bilangan Fibonacci, misalnya 1, 2, 3, 5, 8 dan seterusnya. Bunga matahari misalnya mahkotanya tersusun dengan bilangan Fibonacci yakni 13, 21, 34 hingga 55 mahkota.

Kulit nanas memiliki bentuk heksagonal atau segi enam yang membentuk spiral dalam tiga arah berbeda. Ketika mengamati seti spiral pada biji pinus akan tampak penerapan bilangan Fibonacci yang mana jumlah set spiral semakin banyak saat menurun.

Bagian spiral dari cangkang nautilus bilik dan besar sudutnya membentuk proporsi dari bilangan Fibonacci. Selain pada benda-benda di alam yang terbentuk secara alami tanpa campur tangan manusia, proporsi dari biola Antonio Stradivarius juga membentuk pola bilangan Fibonacci yakni 2, 3, 5, 8 dan 13.

Bilangan Fibonacci

Pola bilangan Fibonacci bisa dituliskan sebagai berikut:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Setiap bilangan setelahnya merupakan penjumlahan dari dua bilangan yang ada di depannya, misal:

Bilangan ke 1: 1 + 1 = 2
Bilangan ke 2: 1 + 2 = 3
Bilangan ke 3: 2 + 3 = 5
Bilangan ke 4: 5 + 3 = 8
Bilangan ke 5: 5 + 8 = 13
Bilangan ke 6: 8 + 13 = 21
Bilangan ke 7: 13 + 21 = 34 dan seterusnya

Untuk membantu memudahkan pemahaman terkait pola Fibonacci, barisan Fibonacci bisa dibuat sebagaimana Gambar 1 di bawah ini.

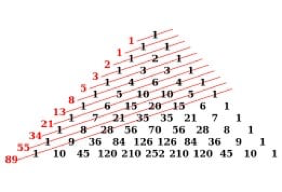
Barisan Fibonacci juga bisa digunakan untuk baris bilangan yang lain seperti pada susunan bilangan di bawah ini:

2, 2, 4, 6, 10, 16, 26, 42, …
3, 6, 9, 15, 24, 39, …

Ciri khas dari bilangan Fibonacci adalah bisa membentuk pola spiral. Misalnya kotak dengan ukuran 1 cm x 1 cm selanjutnya di bagian bawah dibuat kotak berukuran 2 cm x 2 cm yang merupakan penjumlahan dari 1 + 1 = 2.

Di sampingnya lagi dibuat kotak dengan ukuran 3 cm x 3 cm yang merupakan penjumlahan dari 1 + 2 = 3 sehingga membentuk pola spiral.

Deret Fibonacci

Himpunan barisan Fibonacci membentuk pola yang berulang atau rekursif sehingga persamaan barisan Fibonacci dengan dua suku yang pertama yakni F1 = 0 dan F2 = 1 bisa dirumuskan dengan formula berikut ini:

F_{n + 1} = F_{n – 1} + Fn

Rumus di atas dapat digunakan untuk menghitung suku-suku selanjutnya secara berulang atau rekursif.

Rumus Fibonacci

Barisan deret Fibonacci merupakan barisan dengan suku ke n adalah penjumlahan dari dua suku di depannya. Sehingga untuk menentukan angka atau bilangan dari barisan Fibonacci di suku ke n dengan mengurangi suku ke n dengan 1 kemudian ditambahkan dengan pengurangan suku ke n dengan 2.

Un = (n – 1) + (n – 2)

Keterangan:
n = deretan suku ke n

Golden Ratio Bilangan Fibonacci

Deret Fibonacci seperti yang sudah diketahui di atas dapat diteruskan sampai tidak terbatas. Namun, ternyata ada sebuah rahasia alam yang luar biasa ketika nilai deret Fibonacci diteruskan. Konsep ini dinamakan sebagai konsep Golden Ratio atau rasio emas.

Ketika bilangan Fibonacci diteruskan sampai tidak terbatas dan dihitung nilai perbandingan atau rasio di antara dua angka berdekatan pada deret Fibonacci, maka akan diperoleh rasio yang semakin mendekati angka 1,6.

Nilai 1,6 ini disebut sebagai Golden Ratio yang merupakan perbandingan antara bilangan di depannya dengan bilangan sebelumnya. Ketika rasio terus dihitung, maka akan diperoleh nilai mendekati kepastian dari Golden Ratio yang dinotasikan dengan “phi” sebagai berikut:

phi = 1,6180339887…

Contoh Soal Bilangan Fibonacci

1. Tentukan berapakah angka bilangan Fibonacci ke 6 dan ke 12 dari deret baris bilangan Fibonacci di bawah ini:

1, 2, 3, …

Pembahasan

Jawab:

Jika deret balingan Fibonacci di atas dibuat lebih panjang lagi maka akan terbentuk deret berikut ini:

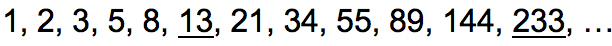
2. Tentukan berapakah lima suku berikutnya dari barisan berikut ini:

a. 3, 4, 7, 11, 18, 29, ….
b. 2, 2, 4, 6, 10, 16, 26, 42, …

Kesimpulan

Himpunan bilangan yang ada pada kehidupan sehari-hari apabila disusun dapat membentuk pola yang teratur dan bersifat tetap. Mempelajari pola bilangan Fibonacci, bisa membantu menentukan berapakah bilangan pada suku ke n. Pola bilangan Fibonacci bisa ditemukan di alam seperti susunan daun bunga.