Lingkaran: Pengertian, Unsur, Rumus, Contoh Soal

Ada banyak benda di lingkungan yang berbentuk lingkaran. Salah satu benda berbentuk lingkaran yang paling sering ditemukan adalah ban kendaraan bermotor dan sepeda. Kendaraan menggunakan ban berbentuk lingkaran karena dapat berputar dengan halus sehingga mempermudah jalan kendaraan.

Pengertian Lingkaran

Lingkaran merupakan sebuah kurva tertutup yang mana seluruh titik pada lingkaran memiliki jarak yang sama pada titik pusatnya yang tetap. Bisa juga dikatakan bahwa lingkaran merupakan kumpulan titik-titik pada garis bidang datar dengan jarak yang sama dari titik tertentu yakni pusat lingkaran.

Dari kumpulan titik-titik tersebut kemudian dihubungkan dengan garis hingga membentuk garis lengkung yang tidak berujung.

Penerapan Lingkaran

Lingkaran termasuk ke dalam objek geometri dua dimensi yang banyak diaplikasikan ke dalam berbagai bidang. Memahami rumus perhitungan luas lingkaran dan keliling lingkaran sangat penting karena bisa digunakan untuk menghitung luas suatu objek seperti lahan berbentuk lingkaran.

Selain itu, beberapa lapangan olahraga ada yang berbentuk satu lingkaran penuh atau setengah lingkaran. Untuk menghitung keliling lapangan dan luas lapangan dibutuhkan pemahaman terkait rumus lingkaran. Aplikasi lingkaran juga banyak diadopsi pada ban kendaraan bermotor, mobil hingga kendaraan sepeda.

Ukuran diameter ban baik ban motor roda dua, ban mobil sudah dihitung oleh pihak pabrik sedemikian rupa sehingga memenuhi standar keamanan yang berlaku. Apabila ukuran ban tersebut diubah, maka tentu dapat menyebabkan bahaya pada pengendara.  

Unsur-Unsur Pada Lingkaran

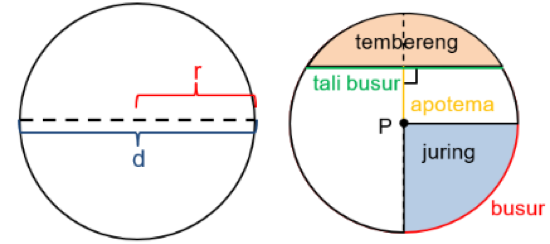
Lingkaran memiliki 8 unsur yakni titik pusat, diameter, jari-jari, tali busur, juring, busur, apotema, dan tembereng.

1. Titik Pusat

Titik pusat adalah titik yang jaraknya sama dengan seluruh titik yang ada di keliling lingkaran. Letak titik pusat ada di tengah-tengah lingkaran umumnya menggunakan lambang O.

2. Jari-Jari (r)

Lingkaran memiliki jari-jari dan diameter yang nilainya tetap meski diukur dari titik lingkaran manapun. Jari-jari dilambangkan dengan symbol r yang nilainya adalah setengah dari diameter. Jari-jari adalah jarak yang diukur dari titik pusat menuju titik pada lingkaran.

3. Diameter (d)

Diameter adalah jarak yang diukur dari satu titik di lingkaran menuju titik lainnya yang melewati titik pusat lingkaran. Nilai diameter adalah dua kali dari jari-jari. 

4. Tali Busur

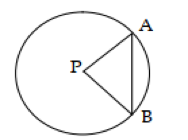
Tali busur merupakan garis yang menghubungkan dua titik pada keliling lingkaran yang tidak melewati titik pusat lingkaran. Garis AB pada gambar di bawah adalah tali busur lingkaran sementara titik P adalah titik pusat. Garis AP dan garis BP adalah jari-jari lingkaran.

5. Juring Lingkaran

Juring lingkaran merupakan luas daerah pada lingkaran yang dibatasi oleh dua buah jari-jari yang dibatasi oleh suatu busur lingkaran. Ada dua juring lingkaran yakni juring kecil dan juring besar

6. Tembereng Lingkaran

Tembereng merupakan luas daerah yang dibatasi oleh tali busur lingkaran dan busurnya.

7. Apotema

Apotema merupakan jarak paling pendek yang diukur antara tali busur dengan titik pusat lingkaran. Tali busur tegak lurus dengan garis apotema.

8. Busur

Busur yaitu garis lengkung yang menjadi bagian dari keliling lingkaran. Ada dua jenis busur lingkaran yakni busur kecil dan busur besar. Busur besar mempunyai panjang lebih dari setengah lingkaran sementara busur kecil mempunyai panjang kurang dari setengahnya.

Pelajari Juga Bangun Datar

Keliling Lingkaran

Keliling lingkaran adalah panjang lintasan yang dilalui oleh suatu benda dari satu titik yang bergerak berjalan searah putaran jarum jam kemudian kembali ketitik awal. Untuk mencari keliling lingkaran bisa dilakukan dengan cara mengalikan π dengan diameter lingkaran atau senilai dua kali jari-jari lingkaran.

K = π x D
K = 2 x π x r

Keterangan:

D = diameter lingkaran
r = jari-jari lingkaran
π = konstanta yang dibaca phi, konstanta bernilai tetap yakni 22/7 atau 3,14

Luas Lingkaran

Luas lingkaran dapat dihitung menggunakan rumus di bawah ini:

L = π x r²
L = 22/7 x r²

Anda juga dapat menghitung luas lingkaran menggunakan data diameter lingkaran.

r = ½ d
d = 2r
L = π x (1/2 d)²
L = 22/7 x 1/4 d²

Persamaan Lingkaran

• Panjang Busur dan Luas Juring Lingkaran

Panjang busur = (Besar sudut pusat/360⁰) x Klingkaran
Luas juring =  (Besar sudut pusat/360⁰) x Llingkaran

• Persamaan Garis Singgung Lingkaran

1. Panjang Garis Singgung dari Titik di Luar Lingkaran

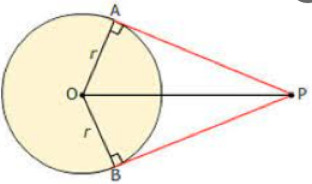
Garis AP merupakan garis singgung sehingga berlaku:
OP² = AP² + OA²

2. Panjang Garis Singgung Persekutuan Dalam Dua Lingkaran

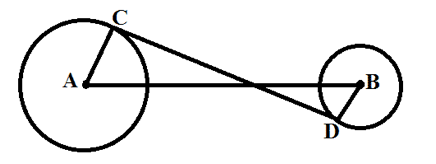
Garis CD merupakan garis singgung persekutuan dalam yang bisa dihitung dengan rumus:

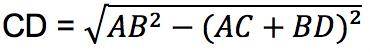
Pelajari Juga Persamaan Garis Lurus & Singgung

Contoh Soal

• Soal 1

Sebuah lingkaran memiliki jari-jari sepanjang 21 cm. Tentukan berapakah luas dan keliling lingkaran tersebut.

• Soal 2

Sebuah lapangan olahraga memiliki luas sebesar 2.464 m², di sekeliling lapangan akan dibangun pagar dari bahan papan kayu dengan lebar 2 m. Tentukan seberapa banyak papan kayu yang dibutuhkan untuk membangun pagar di sekeliling lapangan bundar?

Pembahasan

Diketahui:

L = 2.464 m²
lebar papan kayu (l) = 2 m

Ditanya:

Banyak papan kayu yang dibutuhkan

Jawab:

Pertama-tama harus dicari tahu terlebih dahulu besar jari-jari lingkaran lapangan olahraga

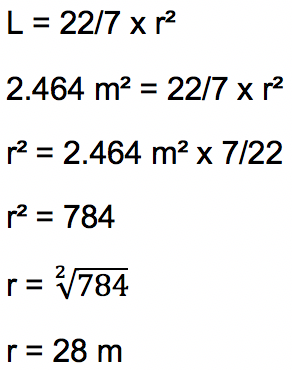
Diperoleh panjang jari-jari (r) adalah 28 m maka bisa dihitung jumlah papan kayu yang dibutuhkan dengan mengukur keliling lingkarannya.

K = 2 x π x r
K = 2 x 22/7 x 28 m
K = 176 m

Selanjutnya cukup dibagi keliling lingkaran dengan lebar papan kayu

Jumlah papan yang dibutuhkan = K : l
Jumlah papan yang dibutuhkan = 176 m : 2 m
Jumlah papan yang dibutuhkan = 88 buah

Sehingga jumlah papan kayu yang diperlukan sebanyak 88 buah

Kesimpulan

Bentuk geometri lingkaran pada ban kendaraan sangat penting karena akan membuat jalan kendaraan menjadi lebih halus. Lingkaran memiliki jumlah simetri putar dan simetri lipat tak terhingga karena bentuknya yang tanpa sudut.