Kekontinuan fungsi trigonometri dapat dibuktikan menggunakan konsep limit fungsi trigonometri dengan nilai x mendekati 0. Untuk melakukan perhitungan limit fungsi, maka digunakan teorema yang lumrah digunakan dalam kalkulus yakni Teorema Apit.

Trigonometri sangat berperan dalam kehidupan manusia. Berbagai aktivitas kehidupan dapat dikaitkan dengan fenomena trigonometri dan penerapan trigonometri. Sebagai contoh, konsep trigonometri dapat digunakan untuk bidang teknologi kedokteran, teori fisika dan juga keteknikan.

Daftar Isi show

Pengertian Trigonometri

Trigonometri merupakan materi dalam Matematika yang membahas mengenai hubungan antara sisi dan juga sudut dari bangun datar segitiga. Istilah trigonometri berasal dari Bahasa Yunan yakni trigonon yang artinya adalah tiga buah sudut. Sementara metron artinya adalah mengukur.

Oleh karena itu rumus trigonometri digunakan untuk menghitung besar sudut dari suatu bangun datar segitiga. Besar sudut segitiga tersebut bisa dihitung hanya bermodalkan informasi besar sisi segitiga tanpa harus mengukurnya secara langsung.

Pengukuran sudut segitiga ini dikenal dengan sin, cos, tan. Istilah sinus (sin), cosinus (cos), tangen (tan) serta turunannya yaitu cosecant (csc), cotangent (cot) dan secan (sec) digunakan dalam pengukuran sudut bangun segitiga melalui perbandingan sisi segitiga.

Misalkan bangun segitiga siku-siku dengan sisi alas a, sisi tinggi b, dan sisi miring c, serta sudut pertemuan sisi alas dengan sisi miring adalah ϴ, maka nilai sinus, cosinus dan tangennya adalah:

sin ϴ = sisi tinggi/sisi miring = b/c
cos ϴ = sisi alas/sisi miring = a/c
tan ϴ = sisi tinggi/sisi alas = b/a

Turunan Trigonometri

Turunan atau disebut diferensial merupakan operasi perhitungan Matematika untuk menghitung perubahan nilai suatu fungsi dikarenakan nilai input pada variabel yang berbeda. Materi turunan bermanfaat dalam menghitung garis singgung kurva fungsi kecepatan, laju pertumbuhan organisme dan sebagainya.

Sementara turunan trigonometri adalah konsep turunan yang didapat dari limit fungsi trigonometri. Berikut adalah turunan dari fungsi trigonometri:

f(y) = sin y maka turunan f’(y) = cos y
f(y) = cos y maka turunan f’(y) = – sin y
f(y) = tan y maka turunan f’(y) = sec² y
f(y) = sin ay maka turunan f’(y) = a cos ay
f(y) = cos ay maka turunan f’(y) = – a sin ay
f(y) = sec y maka turunan f’(y) = sec y tan y
f(y) = cotan y maka turunan f’(y) = -cosec² y
f(y) = cosec y maka turunan f’(y) = – cosec y cotan y

Apabila turunan trigonometri melibatkan persamaan atau fungsi tertentu, misalnya u adalah fungsi yang bisa diturunkan terhadap variabel y, maka u’ adalah turunan u terhadap y, maka turunannya berlaku sebagai berikut:

f(y) = sin u maka turunan f’(y) = u’ . cos u
f(y) = cos u maka turunan f’(y) = -u’ . sin u
f(y) = tan u maka turunan f’(y) = u’ . sec² u
f(y) = sec u maka turunan f’(y) = u’ sec u tan u
f(y) = cotan u maka turunan f’(y) = – u’ cosec² u
f(y) = cosec u maka turunan f’(y) = – u’ cosec u cotan u

Contoh:

Turunan dari fungsi trigonometri f(x) = sin (cx + h) maka turunan f’(x) = c cos (cx + h)

Limit Fungsi Trigonometri

Dalam Matematika, limit fungsi diartikan sebagai pergerakan nilai fungsi mendekati batasan nilai tertentu yang paling mendekati nilai tersebut namun tidak pernah mencapai nilai tertentu tersebut secara tepat. Penulisan limit fungsi secara umum menggunakan notasi berikut:

Untuk membuktikan limit fungsi trigonometri maka digunakan Teorema Apit. Misal terdapat fungsi h, i, j yang terdefinisi pada interval terbuka L yang memuat a kecuali di a itu sendiri, sehingga berlaku fungsi h(x) ≤ i(x) ≤ j(x) untuk setiap x ϵ L dan x a.

Sehingga berdasarkan Teorema Apit di atas terbukti bahwa nilai limit fungsi trigonometri berikut ini:

Sehingga disimpulkan teorema limit fungsi trigonometri untuk sembarang nilai real a, diperoleh:

Contoh Soal Limit Trigonometri

Soal 1

Tentukan nilai limit fungsi trigonometri di bawah ini:

Pembahasan

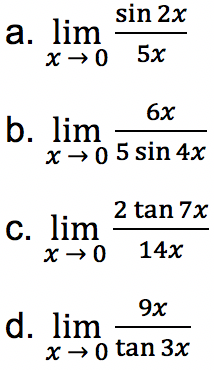
Jawab:

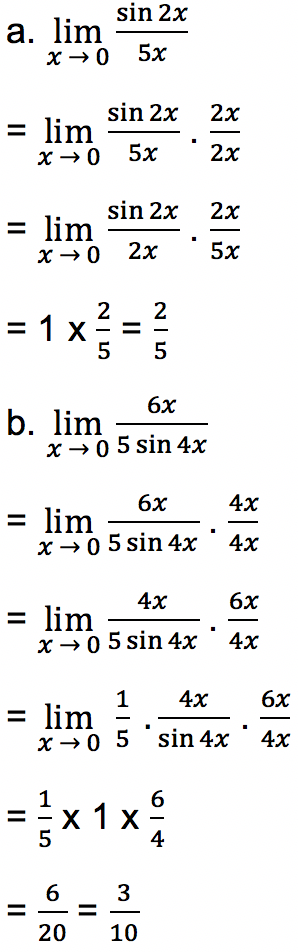
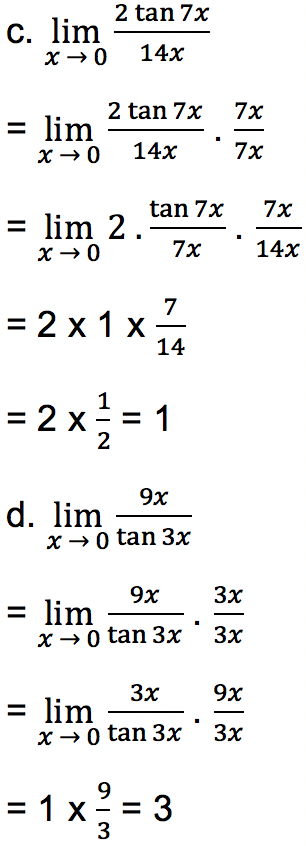
Soal 2

Tentukan limit fungsi trigonometri di bawah ini:

Pembahasan

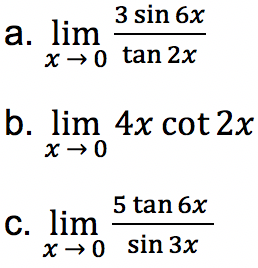
Jawab:

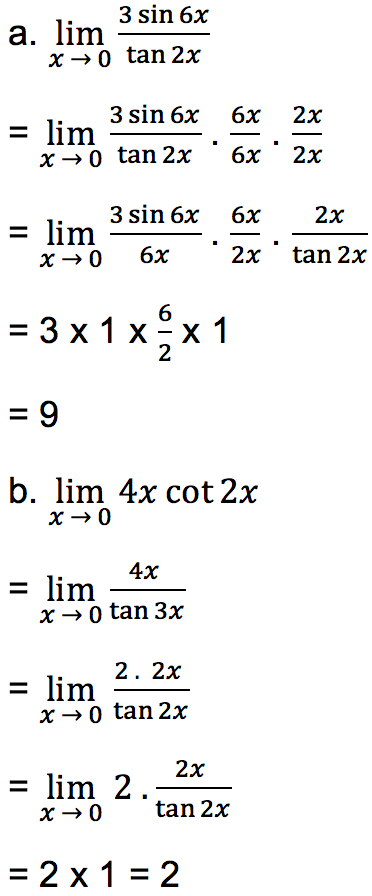
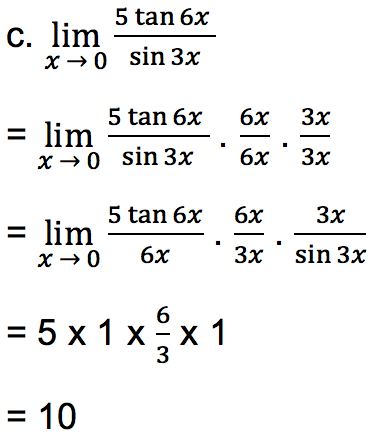
Soal 3

Tentukan limit dari fungsi trigonometri di bawah ini:

Pembahasan

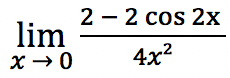
Jawab:

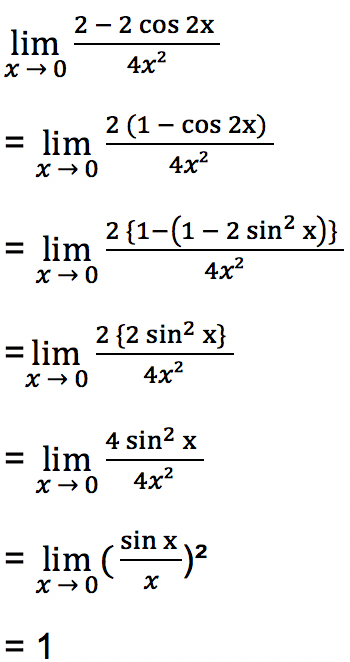
Limit fungsi trigonometri adalah pergerakan nilai fungsi trigonometri mendekati batasan nilai tertentu yang paling mendekati nilai tersebut namun tidak tepat mencapai nilai tersebut.