Fungsi Komposisi: Definisi, Sifat, Rumus, dan Contoh Soal

Fungsi komposisi merupakan salah satu bagian dari materi fungsi dalam Matematika yang wajib untuk dipelajari dan dipahami. Fungsi sendiri merupakan relasi yang menghubungkan dua buah himpunan dengan setiap anggota domain dipasangkan tepat satu anggota kodomain.

Pengertian Fungsi Komposisi

Fungsi termasuk salah satu relasi dalam Matematika yang memasangkan semua anggota dari himpunan asal ke himpunan kawan tepat satu anggota saja. Seringkali pada kehidupan nyata, fungsi-fungsi yang berbeda menghubungkan berbagai himpunan yang saling berhubungan satu dengan lainnya.

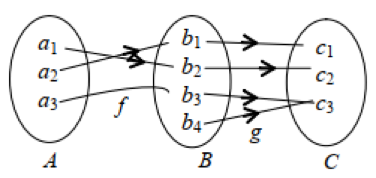
Sebuah fungsi yang menghubungkan dua buah himpunan kemudian dilanjutkan dengan fungsi lain yang menghubungkan himpunan kodomain pertama sebagai himpunan domain akan membentuk sebuah fungsi baru.

Hal ini bisa dilihat pada Gambar 1 di atas yang mana himpunan A dihubungkan oleh fungsi f ke himpunan B. Selanjutnya himpunan B sebagai domain dihubungkan oleh fungsi g ke himpunan C. Fungsi f dan g ini membentuk fungsi baru yang disebut sebagai fungsi komposisi.

Operasi fungsi komposisi dilambangkan dengan notasi “o” yang dibaca sebagai komposisi atau bundaran. Fungsi komposisi yang bisa dibuat untuk memetakan himpunan A ke himpunan C secara langsung adalah fungsi g komposisi f atau dinotasikan dengan tanda (g o f) (x).

Arti dari tanda (g o f) (x) adalah fungsi yang dipetakan oleh f(x) kemudian dilanjutkan lagi dengan fungsi g(x). Sehingga cara mengoperasikannya adalah dengan mengerjakan fungsi f(x) terlebih dulu kemudian hasil pengoperasiannya dimasukkan ke fungsi g(x).

Dengan mengoperasikan fungsi komposisi maka akan terbentuk suatu fungsi tunggal. Fungsi tunggal merupakan fungsi baru yang terbentuk dari fungsi komposisi dan bisa ditulis dengan notasi baru misal pada (g o f) (x) = h(x), maka h(x) adalah fungsi tunggal.

Sifat-Sifat Fungsi Komposisi

Fungsi komposisi mempunyai beberapa sifat yang harus dipahami ketika mengerjakannya sebagai berikut:

1. Fungsi komposisi tidak komutatif, yakni fungsi komposisi apabila letak fungsi yang dimasukkan kepada fungsi lainnya berbeda maka fungsi baru yang dihasilkan berbeda.
   (g o f) (x) ≠ (f o g) (x)

2. Fungsi komposisi bersifat asosiatif, yakni sifat operasi matematika terhadap 3 bilangan atau dalam hal ini 3 fungsi yang mana dua fungsi dikelompokkan untuk dikerjakan terlebih dulu. Fungsi komposisi bersifat asosiatif sehingga pengelompokan pada fungsi-fungsinya akan memberikan hasil yang sama.
   (f o (g o h)) (x) = ((f o g) o h) (x)

3. Fungsi komposisi mempunyai fungsi identitas yang dilambangkan dengan I(x) yang mana berlaku sifat komposisi antara fungsi tersebut dengan fungsi identitasnya akan menghasilkan fungsi itu sendiri.
   (f o I) (x) = (I o f) (x) = f(x)

Rumus Fungsi Komposisi

Rumus fungsi komposisi berangkat dari definisi fungsi komposisi itu sendiri yakni fungsi yang dipetakan pertama dioperasikan lebih dulu baru kemudian hasilnya dimasukkan ke fungsi berikutnya. Pada fungsi komposisi g bundaran f atau fungsi g komposisi f dinotasikan (g o f) (x) dikerjakan dengan cara berikut:

• (g o f) (x) = g (f(x))

Artinya f dimasukkan ke fungsi g terlebih dulu kemudian dioperasikan

• (f o g) (x) = f (g(x))

Artinya g dimasukkan ke fungsi f terlebih dulu kemudian dioperasikan

Syarat fungsi f dan g bisa dikomposisikan (f o g) (x)  adalah jika daerah hasil dari g merupakan himpunan bagian dari daerah asalnya dari fungsi f.

Pemanfaatan Fungsi Komposisi dalam Kehidupan

Proses pendauran ulang logam memanfaatkan prinsip dalam fungsi komposisi. Pada proses daur ulang logam, pecahan logam campuran dihancurkan hingga menjadi serpihan-serpihan kecil terlebih dahulu. Selanjutnya drum magnetik yang ada di dalam mesin penghancur akan memisahkan logam.

Drum magnetik tersebut akan mengambil logam magnetik yang mengandung unsur besi dan memisahkannya dari logam lain tanpa unsur besi. Sisa dari pecahan logam pun dikeruk dan dipisahkan. Logam dengan unsur besi dilebur menjadi baja baru. Seluruh prinsip daur ulang ini menerapkan konsep fungsi komposisi.

Soal dan Pembahasan

1. Diketahui fungsi g(x) = 4x – 3 dan fungsi f(x) = 5x + 7, maka tentukan berapakah fungsi (g o f) (x) dan (f o g) (x).

2. Diketahui fungsi h(x) = x – 5, tentukan berapakah fungsi j(x) apabila:

a. (h o j) (x) = 4x + 1
b. Dengan fungsi j(x) yang sudah diperoleh, tentukan berapakah nilai dari (j o h) (2)

3. Diketahui fungsi h(x) = 2x + 13, fungsi k(x) = x² + 2 serta f(x) = 13x – 2. Tentukan berapakah (h o (k o f)) (x).

Kesimpulan

Fungsi komposisi adalah operasi fungsi yang menghubungkan dua buah fungsi yang bekerja di lebih dari 2 himpunan. Fungsi komposisi akan menggabungkan dua jenis fungsi menjadi suatu fungsi baru yang disebut fungsi tunggal. Notasi fungsi komposisi memakai simbol “o” yang dibaca komposisi atau bundaran.