Belah ketupat termasuk ke dalam salah satu jenis bangun datar yang memiliki dua dimensi yakni dimensi panjang dan lebar. Ada beberapa komponen pada bangun datar yakni panjang sisi, sudut, luas, keliling dan diagonal. Oleh karena itu sangat penting dalam memahami komponen pada setiap bangun datar.
Definisi Belah Ketupat
Belah ketupat merupakan bangun datar segiempat dengan keempat buah ruas sisinya yang sama panjang. Bisa dikatakan bahwa bangun datar belah ketupat merupakan segiempat yang kedua diagonalnya saling tegak lurus serta saling membagi diagonal dengan dua sama panjang.
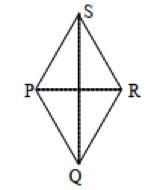
Bangun belah ketupat PQRS di atas memiliki empat buah sisi yakni sisi PS, sisi SR, sisi QR dan sisi PQ. Di tengah belah ketupat terdapat dua buah diagonal yang berpotongan saling tegak lurus yakni diagonal PR dan QS. Diagonal PR dan QS memiliki ukuran yang tidak sama panjang.
Belah Ketupat dalam Kehidupan Sehari-Hari
Seperti namanya, aplikasi objek geometri belah ketupat bisa ditemukan dalam berbagai kehidupan sehari-hari, yang paling mudah dilihat adalah pada pembuatan ketupat saat lebaran. Ketupat ketika digantung membuat bentuk belah ketupat yang sangat unik.
Selain pada ketupat, bentuk belah ketupat juga bisa ditemukan pada rambu-rambu lalu lintas dengan dasarnya berbentuk belah ketupat. Desain geometri pada candi seperti lubang dan celah-celahnya paling banyak menggunakan bentuk belah ketupat.
Sifat-Sifat Belah Ketupat
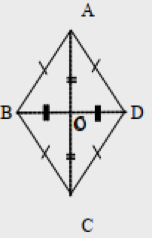
Belah ketupat merupakan salah satu bangun datar segi empat yang memiliki beberapa sifat-sifat sebagai berikut:
- Seluruh sisi bangun datar belah ketupat kongruen. Makna kongruen adalah ketika sisi bangun datar mempunyai bentuk serta ukuran yang sama.
- Sisi-sisi pada belah ketupat yang saling berhadapan sejajar yakni pada gambar di atas adalah sisi AB // CD dan sisi AD // BC.
- Sudut-sudut pada belah ketupat yang saling berhadapan kongruen. Sudut pada belah ketupat bukan merupakan sudut siku-siku
- Diagonal pada belah ketupat akan membagi sudut menjadi dua ukuran yang sama besar yakni:
- sudut ABO = sudut CBO = ½ sudut ABC
- sudut ADO = sudut CDO = ½ sudut ADC
- sudut BAO = sudut DAO = ½ sudut BAD
- sudut BCO = sudut DCO = ½ sudut BCD
- Kedua diagonal belah ketupat saling tegak lurus serta saling membagi diagonal-diagonalnya dengan ukuran sama panjang.
- Kedua diagonal dari belah ketupat merupakan sumbu simetri sehingga diagonal membagi belah ketupat menjadi dua bagian yang sama besar yakni ∆ABC = ∆ADC dan ∆BCD = ∆BAD.
- Jumlah ukuran dua sudut belah ketupat yang berdekatan sebesar 180⁰, yakni
- sudut ABC + sudut BAD = 180⁰
- sudut ADC + sudut BCD = 180⁰
- sudut ABC + sudut DCB = 180⁰
- sudut CDA + sudut BAD = 180⁰
Rumus Belah Ketupat
- Keliling Belah Ketupat
Keliling bidang datar belah ketupat merupakan hasil penjumlahan dari keempat panjang sisinya.
K = 4 x s
s = sisi belah ketupat
- Luas Belah Ketupat
Luas daerah bidang datar belah ketupat sama dengan setengah dari hasil kali ruas diagonal-diagonalnya.
L = ½ x d1 x d2
Keterangan:
L = Luas daerah belah ketupat
d1 = diagonal 1 belah ketupat
d2 = diagonal 2 belah ketupat
Untuk menghitung luas belah ketupat sebenarnya bisa dilakukan dengan cara menggunakan rumus luas segitiga. Hal ini karena belah ketupat terdiri dari dua buah segitiga sama kaki.
Pelajari Juga Layang-Layang
Contoh Soal
- Contoh 1
Belah ketupat PQRS memiliki panjang diagonal PR = 10 satuan panjang, QS = 12 satuan panjang dan PS = 6 satuan panjang. Tentukan berapa keliling dan juga luas daerah belah ketupat PQRS.
Diketahui:
PR = 10 satuan panjang (d1)
QS = 12 satuan panjang (d2)
PS = 6 satuan panjang
Ditanya:
Luas dan keliling belah ketupat PQRS
Jawab:
Untuk mencari luas belah ketupat menggunakan rumus berikut ini:
L = ½ x d1 x d2
L = ½ x 10 x 12
L = 60 satuan luas
Untuk mencari keliling belah ketupat PQRS menggunakan rumus di bawah ini:
K = 4 x PS
K = 4 x 6 = 24
- Contoh 2
Sebuah belah ketupat ABCD memiliki bentuk dan ukuran ruas seperti gambar di bawah ini. Diketahui bahwa panjang ruas AO sebesar 3,5 cm dan panjang ruas OB sebesar 2 cm. Tentukan berapa luas daerah belah ketupat berikut.
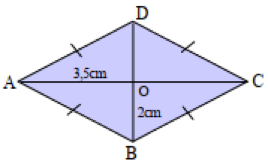
Diketahui:
AO = ½ diagonal AC = 3,5 cm
OB = ½ diagonal BD = 2 cm
Ditanya:
Luas daerah belah ketupat
Jawab:
Untuk menghitung luas daerah belah ketupat harus diketahui terlebih dahulu panjang kedua diagonal. Diketahui bahwa diagonal belah ketupat saling tegak lurus dan membagi satu sama lainnya dengan dua sama panjang. Sehingga:
Diagonal AC (d1) = 3,5 x 2 = 7
Diagonal BD (d2) = 2 x 2 = 4
L = ½ x d1 x d2
L = ½ x 7 x 4
L = 14 cm²
Sehingga luas daerah belah ketupat PQRS sebesar 60 satuan luas dengan keliling sebesar 24 satuan panjang
- Contoh 3
Tentukan besar sudut di bawah ini:
a. Apabila ukuran sudut ABC = 132⁰, tentukan berapa besar sudut ABD
b. Apabila ukuran sudut BDC = 25⁰, tentukan berapa besar sudut ADC
c. Apabila ukuran sudut EBC = (2y + 10)⁰, tentukan berapa nilai y
d. Apabila ukuran sudut ADE = (5x – 20)⁰ tentukan berapa nilai x
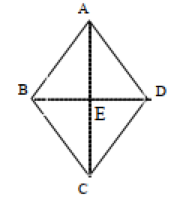
Jawab:
a. Diketahui bahwa diagonal pada belah ketupat akan membagi sudut menjadi dua ukuran yang sama besar sehingga sudut ABD = ½ ABC.
Sudut ABD = ½ x 132⁰
Sudut ABD = 66⁰
b. Besar sudut BDC adalah ½ dari sudut ADC sehingga untuk mencari sudut ADC menggunakan persamaan berikut:
sudut ADC = 2 x sudut BDC
sudut ADC = 2 x 25⁰ = 50⁰
c. Diketahui besar sudut EBC = sudut ABD
(2y + 10)⁰ = = 66⁰
2y = 66⁰ – 10⁰
2y = 56⁰
y = 28⁰
d. sudut ADE = sudut BDC sehingga
(5x – 20)⁰ = 25⁰
5x = 25⁰ + 20⁰
5x = 45⁰
x = 9
Kesimpulan
Belah ketupat termasuk bangun datar dua dimensi yang keempat sisinya sama panjang. Bentuk belah ketupat seperti dua buah segitiga yang digabungkan. Belah ketupat punya dua buah diagonal yang berpotongan saling tegak lurus. Aplikasi belah ketupat bisa ditemukan di kehidupan seperti pada candi.
