Dalam matematika, konsep suku banyak atau yang lumrah dikenal sebagai polinomial merupakan fungsi Matematika yang di dalamnya terdapat operasi hitung penjumlahan, pengurangan, perkalian dan pangkat bilangan bulat bernilai positif.
Peraturan mengenai suku banyak sangat membantu dalam mengerjakan berbagai tugas keseharian yang melibatkan variabel tertentu. Agar lebih memahami materi polinomial, sebaiknya sering berlatih contoh soal suku banyak yang disertai pembahasannya seperti di bawah ini.
Pengertian Polinomial
Polinomial atau lebih dikenal sebagai suku banyak adalah bentuk matematika yang di dalamnya melibatkan satu suku atau lebih dengan pangkat variabel tersebut bernilai positif dan bilangan bulat. Dalam materi suku banyak, operasi hitung yang dilibatkan hanyalah pengurangan dan penjumlahan.
Pada suku banyak, variabel-variabel dari setiap suku memiliki pangkat dengan besaran tertentu. Pangkat paling tinggi disebut sebagai derajat. Sementara untuk variabel suku banyak sendiri tidak harus satu namun bisa jadi lebih dari satu variabel dengan berbagai huruf.
Berikut adalah bentuk umum dari suku banyak:
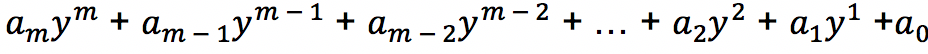
Keterangan:

Dari bentuk umum di atas dapat dilihat bahwa bentuk umum polinomial terdiri dari banyak suku yang mana setiap suku terdiri atas koefisien, variabel ataupun konstanta. Penulisan suku banyak dimulai dari suku yang mempunyai derajat pangkat paling tinggi kemudian terus mengecil pangkatnya hingga pangkat nol.
Pembagian Polinomial
Pembagian suku banyak f(x) berderajat m dibagi dengan fungsi berderajat satu akan memberikan hasil bagi berderajat (m – 1) serta sisa pembagian yang berbentuk konstanta. Pembagian suku banyak dengan pembagi (x – h) bisa menggunakan metode pembagian biasa, skema Horner dan koefisien tak tentu.
Metode Pembagian Biasa
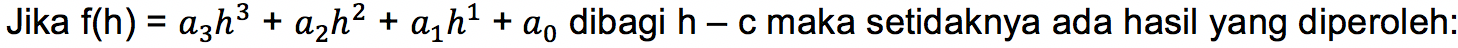
1. Sisa pembagiannya yaitu
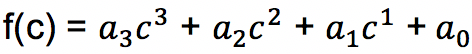
2. Koefisien dari hasil bagi
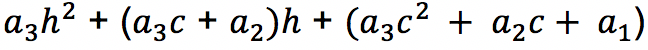
tepat sama dengan bilangan yang ada di baris paling bawah di perhitungan pertama tanpa f(c)
3. Jumlah dari derajat pembagi serta derajat hasil bagi sama dengan derajat terbagi. Derajat sisa terbesar satu lebih kecil dari derajat pembaginya.
Berikut contoh cara pengerjaan pembagian suku banyak
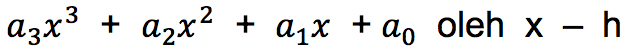
untuk memudahkan pemahaman:
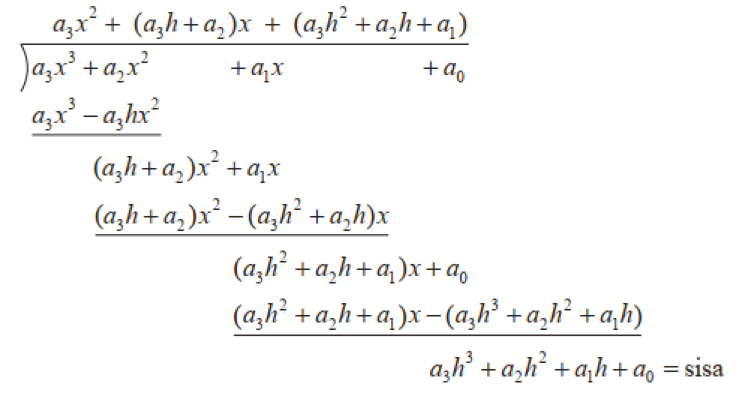
Metode Horner
Metode Horner digunakan untuk menghitung hasil pembagian suku banyak. Skema Horner juga bisa digunakan sebagai alternative untuk menghitung nilai suku banyak selain menggunakan metode substitusi biasa.
Skema Horner cocok untuk bentuk suku banyak yang panjang. Untuk mengerjakan suku banyak menggunakan metode Horner, berikut langkahnya:
Misalkan terdapat bentuk suku banyak f(y) = ay³ + by² + cy + d yang ingin dihitung nilai suku banyak y = h, maka ada 3 langkah yang bisa dilakukan:
- Langkah pertama
Koefisien a dikalikan dengan h kemudian hasilnya dijumlahkan dengan b, seperti berikut:
ah + b
- Langkah kedua
Selanjutnya ah + b dikali dengan h serta hasilnya dijumlahkan dengan c, seperti berikut:
ah² + bh + c
- Langkah ketiga
Selanjutnya ah² + bh + c dikali dengan h serta hasilnya dijumlahkan dengan d, seperti berikut:
ah³ + bh² + ch + d
Secara singkat urutan pengerjaan suku banyak dengan metode Horner jika dituliskan menjadi:
f(y) = ay³ + by² + cy + d
f(y) = (ay² + by + c) y + d
f(y) = ((ay + b) y + c) y + d
Sehingga f(h) = ((ah + b) h + c) h + d
Proses perkalian dan penjumlahan suku banyak
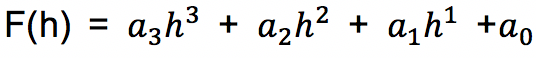
metode Horner bisa digambarkan dengan skema berikut:
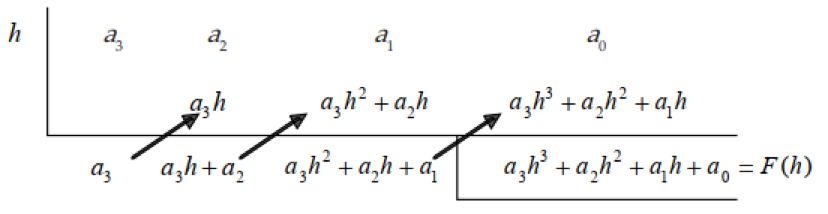
Untuk membandingkan hasil pembagian dengan metode Horner dan pembagian suku banyak dengan algoritma pembagian, maka dimisalkan bentuk suku banyak
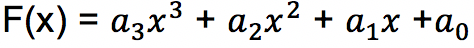
dibagi oleh (x – h) maka cara pembagiannya dengan algoritma pembagian seperti metode pembagian biasa di atas.
Bisa dilihat dari contoh di atas bahwa cara Horner untuk menentukan nilai suku banyak juga bisa digunakan untuk menentukan hasil pembagian serta sisa dari pembagian yang menggunakan pembagi (x – h). Hasil pembagian baik dengan cara algoritma pembagian atau metode Horner menghasilkan hasil yang sama:

Metode Koefisien Tak Tentu
Metode koefisien tak tentu adalah metode lain yang bisa digunakan untuk menghitung hasil pembagian suku banyak. Caranya adalah dengan mensubstitusi f(x) berderajat n dengan g(x) berderajat m ke dalam bentuk umum dari pembagian polinomial. Selanjutnya h(x) serta j(x) diisi dengan:
h(x) adalah polinomial berderajat k, dengan k = n – m
j(x) adalah polinomial berderajat m – k
Contoh Soal Polinomial
- Soal 1
Gunakan metode Horner untuk menghitung hasil pembagian dari:
a. 2x³ + 4x² – 20 dibagi oleh x – 3
b. 2x³ + 5x + 5 dibagi x + 1
Jawab:
a. 2x³ + 4x² – 20 dibagi oleh x – 3

Sehingga berdasarkan metode Horner di atas didapatkan hasil bagi 2x² + 10x + 30 berderajat 2 dengan 70 adalah sisa pembagian.
b.

hasil bagi 2x² – 2x + 7 berderajat 2 dengan 19 adalah sisa pembagian.
- Soal 2
Tentukan hasil pembagian dari 2x³ + 7x² – 13 dengan x – 2
Jawab:
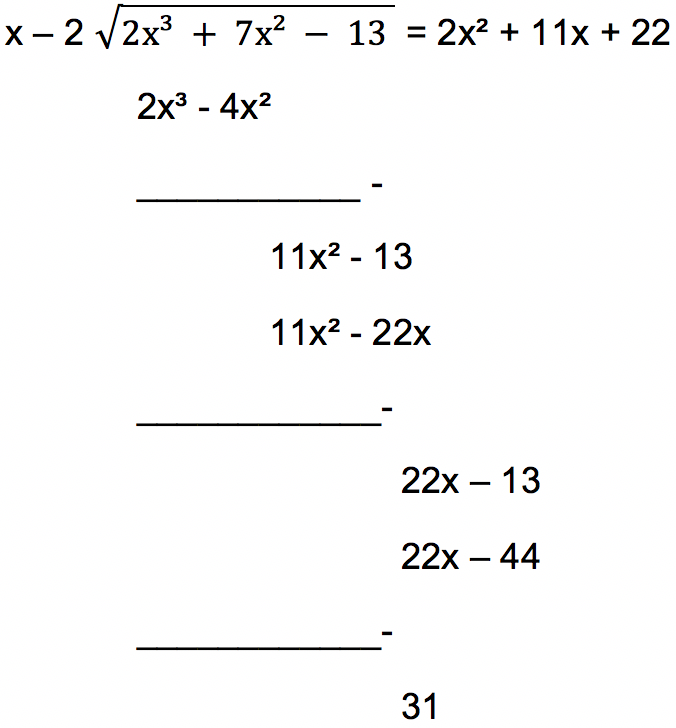
Sehingga dari operasi pembagian di atas bisa dituliskan secara berturut-turut sebagai berikut:
2x³ + 7x² – 13
= (x – 2) 2x² + 11x² – 13
= (x – 2) 2x² + 11x (x – 2) + 22x – 13
= (x – 2) 2x² + 11x (x – 2) + (x – 2) 22 + 31
= (x – 2) (2x² + 11x + 22) + 31
Sisa pembagian adalah 31 yang mana berderajat lebih kecil dibandingkan (x – 2).
Untuk menghitung nilai polinomial sebenarnya bisa dilakukan dengan metode substitusi biasa. Namun, cara substitusi hanya cocok untuk suku banyak yang sederhana. Selain metode substitusi, nilai suku banyak bisa dihitung dengan metode Horner, dan sebagainya.
