Materi turunan dalam Matematika memainkan peranan penting dalam penentuan garis singgung sebuah kurva dari fungsi. Materi turunan akan menjadi dasar dalam memahami teori kalkulus diferensial yang masih berhubungan dengan limit. Contoh soal turunan meliputi turunan akar, fungsi aljabar, dan lainnya.
Dalam setiap contoh soal turunan umumnya turunan dari fungsi tertentu akan dinotasikan menggunakan tanda petik satu setelah nama fungsi. Misalnya turunan dari fungsi g dinotasikan dengan g’. Notasi fungsi turunan g’ mempunyai nilai di titik x dinotasikan dengan g’ (x).
- Soal 1
Diberikan suatu fungsi f (x) = 11x². Tentukan berapakah turunan pertama dari fungsi f (x) tersebut.
Fungsi f (x) = 11x² adalah contoh bentuk fungsi kuadrat yang jika dilukis bentuk kurvanya melengkung ke atas. Kurva melengkung akan memiliki garis singgung di sepanjang kurva. Oleh karenanya gradient garis singgungnya berbeda di setiap titik kurva.
Berikut adalah cara menjawab contoh soal turunan di atas dengan pembahasan lengkap yang diturunkan dari teorinya langsung.
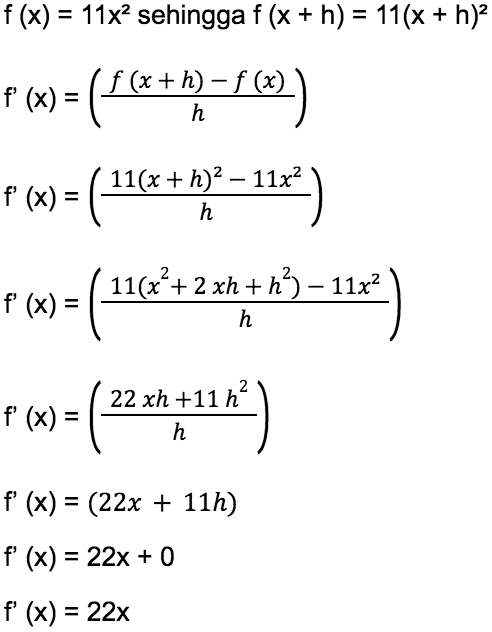
- Soal 2
Diketahui suatu fungsi
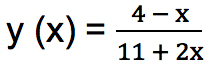
tentukan berapakah turunan dari fungsi y (x).
Untuk mengerjakan soal turunan dari fungsi yang berbentuk pecahan, maka menggunakan rumus di bawah ini:
Dimisalkan bentuk fungsi di atas adalah:

- Soal 3
Tentukan berapakah turunan f’ (x) dari beberapa fungsi berikut ini:
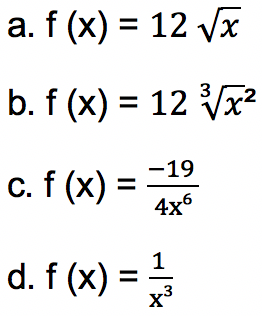


- Soal 4
Suatu fungsi g (x) dituliskan sebagai 5x⁵ – 12x⁴ – 3x³ + x + 10. Tentukan berapakah turunan dari fungsi g (x).
g (x) = 5x⁵ – 12x⁴ – 3x³ + x + 10
g’ (x) = 5 (5) x⁵ˉ¹ – 12 (4)x⁴ˉ¹ – 3 (3) x³ˉ¹ + 1 (1) x¹ˉ¹ + 0
g’ (x) = 25x⁴ – 48x³ – 9x² + 1
- Soal 5
Suatu fungsi h (x) dituliskan sebagai h (x) = (2x⁵ – 6x³) (3x⁴ + 11x²). Tentukan berapakah turunan fungsi h’ (x).
Contoh soal turunan di atas melibatkan teorema turunan untuk fungsi perkalian, sehingga turunan fungsi tersebut harus memenuhi rumus di bawah ini:
h’ (x) = g’ (x) . f (x) + f’ (x) . g (x)
Pada soal di atas dimisalkan bahwa g (x) = (2x⁵ – 6x³) dan f (x) = (3x⁴ + 11x²), maka turunan h’ (x) menjadi:
g’ (x) = 10x⁴ – 18x²
f’ (x) = 12x³ + 22x
h’ (x) = g’ (x) . f (x) + f’ (x) . g (x)
h’ (x) = (10x⁴ – 18x²) . (3x⁴ + 11x²) + (12x³ + 22x) . (2x⁵ – 6x³)
h’ (x) = (30x⁸ + 110x⁶ – 54x⁶ – 198x⁴) + (24x⁸ – 72x⁶ + 44x⁶ – 132x⁴)
h’ (x) = (30x⁸ + 24x⁸) + (110x⁶ – 72x⁶ + 44x⁶ – 54x⁶) + (- 198x⁴ – 132x⁴)
h’ (x) = 54x⁸ + 28x⁶ + – 330x⁴
- Soal 6
Tentukan berapakah nilai f’ (5) untuk fungsi
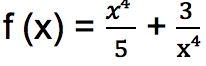
Untuk menghitung nilai f’ (5), maka pertama-tama dihitung terlebih dahulu turunan fungsi f (x) dengan rumus berikut:
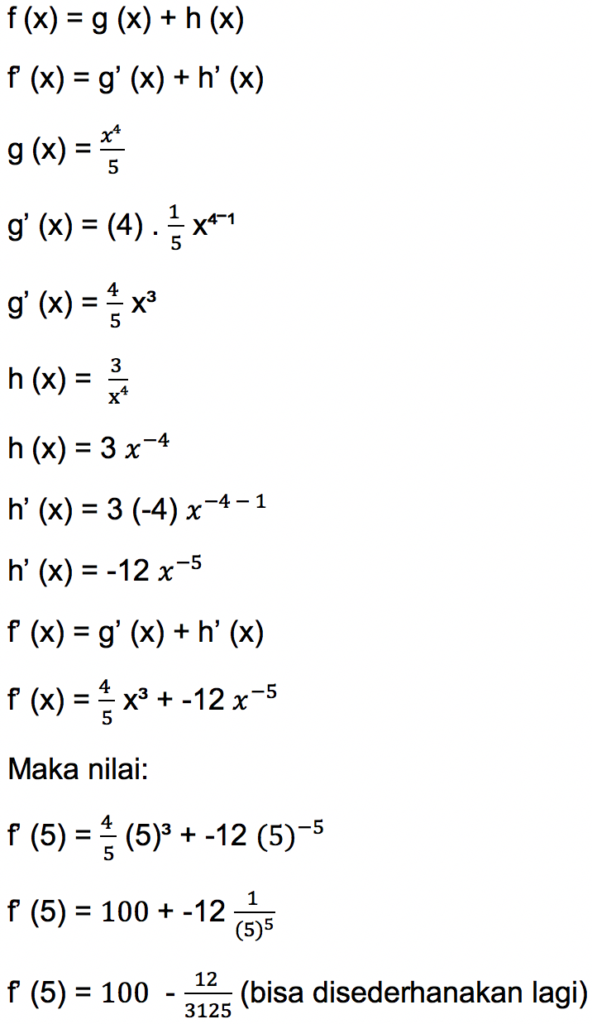
- Soal 7
Tentukan turunan pertama dari fungsi:
a. h (x) = 5x³ + 7x² – 11x
b. h (x) = (2x + 3) (4x + 5)
a. h (x) = 5x³ + 7x² – 11x
h’ (x) = 5 (3) x² + 7 (2) x – 11
h’ (x) = 15x² + 14x – 11
b. h (x) = (2x + 3) (4x + 5)
h (x) = (2x . 4x) + (2x . 5) + (4x . 3) + (3 . 5)
h (x) = (8x²) + (10x) + (12x) + 15
h (x) = 8x² + 22x + 15
h’ (x) = 16x + 22
Dengan berlatih banyak contoh soal turunan yang disertai pembahasan, maka pelajar akan lebih paham mengenai penggunaan rumus turunan untuk soal yang berbeda-beda. Agar dapat mengerjakan soal turunan, maka teorema turunan seperti turunan fungsi perkalian dan lainnya harus dipahami mendalam.
