Selain bentuk persamaan linear, di bangku sekolah juga dipelajari bentuk pertidaksamaan linear. Pertidaksamaan linear yaitu bentuk kalimat terbuka yang kedua sisi dihubungkan tanda pertidaksamaan. Pertidaksamaan banyak dijumpai dalam kehidupan sehari-hari seperti persyaratan kerja dan lainnya.
Definisi Pertidaksamaan Linear
Pertidaksamaan linear adalah kalimat terbuka yang dihubungkan menggunakan tanda
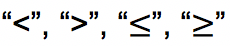
di ruas kanan dan kiri. Pertidaksamaan linear bisa dibedakan menjadi pertidaksamaan linear satu variabel, dua variabel, tiga variabel dan sebagainya.
Jenis pertidaksamaan linear dibedakan berdasarkan jumlah variabel yang terdapat pada persamaan tersebut. Semua pertidaksamaan linear akan memuat variabel.
Solusi atau penyelesaian terhadap pertidaksamaan linear merupakan nilai variabel atau pengganti variabel yang membuat pertidaksamaan bernilai benar. Sebagai contoh pada pertidaksamaan 2x – 5 < 2 – x memiliki nilai x = -5.
Berikut adalah penjelasan pembuktiannya:
2 (-5) – 5 < 2 – (-5)
-10 – 5 < 2 + 5
-15 < 7 adalah pernyataan yang bernilai benar
Penerapan Pertidaksamaan Linear
Dalam kehidupan sehari-hari sebenarnya ada banyak sekali konsep pertidaksamaan linear yang dijumpai tanpa kita sadari. Pertidaksamaan linear yang memberikan pembatasan terhadap sesuatu hal sering dijumpai pada pengumuman lowongan pekerjaan.
Pengumuman lowongan pekerjaan akan mensyaratkan pelamar kerja dengan batas usia tertentu supaya dapat diterima bekerja. Dalam ujian juga terdapat batas nilai yang menentukan apakah siswa lulus ujian atau tidak.
Maksimal laju kendaraan yang boleh melewati suatu jalan raya juga menggunakan sistem pertidaksamaan linear. Pembatasan-pembatasan seperti ini termasuk pertidaksamaan linear.
Pertidaksamaan Linear Satu Variabel
Pertidaksamaan linear satu variabel adalah pertidaksamaan yang hanya memiliki satu peubah atau variabel dengan pangkat tertinggi variabel sebesar satu (linear). Pertidaksamaan linear satu variabel merupakan persamaan yang memiliki bentuk di bawah ini:
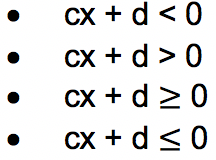
Diketahui:

Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel adalah pertidaksamaan yang memiliki dua peubah atau variabel dengan pangkat tertinggi variabel sebesar satu (linear). Pertidaksamaan linear satu variabel merupakan persamaan yang memiliki bentuk di bawah ini:
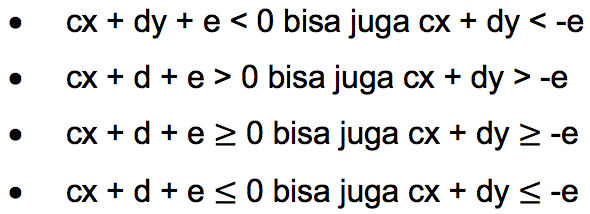
Diketahui:

Sistem Pertidaksamaan Linear
Sistem pertidaksamaan linear merupakan sebuah sistem yang terdiri dari lebih dari satu pertidaksamaan linear sehingga bisa dibuat model matematika dan dicari solusi permasalahan tersebut.
Harus diketahui bahwa pada pertidaksamaan linear berlaku beberapa sifat berikut ini:
- Pengurangan dan penambahan bilangan pada kedua ruas pertidaksamaan, yakni ruas kanan dan kiri, tidak akan mengubah solusi dari pertidaksamaan linear bilangan tersebut. Pertidaksamaan linear baru diperoleh ketika kedua ruas dikurang atau ditambah oleh bilangan yang sama. Pertidaksamaan baru yang dihasilkan disebut sebagai pertidaksamaan linear yang setara atau ekuivalen.
- Perkalian bilangan tidak nol pada kedua ruas, yakni ruas kanan dan kiri pada pertidaksamaan linear, tidak mengubah solusi dari pertidaksamaan linear bilangan tersebut.
- Apabila kedua ruas pertidaksamaan linear dikalikan atau dibagi dengan bilangan negatif yang sama (bukan bilangan nol), membuat tanda pertidaksamaan akan berubah menjadi sebaliknya.
- Apabila kedua ruas pertidaksamaan linear dikalikan atau dibagi dengan bilangan positif yang sama (bukan bilangan nol), tanda pertidaksamaan tidak akan berubah (tetap).
Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel adalah sistem yang terdiri dari lebih dari satu pertidaksamaan linear dengan dua peubah (variabel) sehingga sistem tersebut dapat dibuat model matematika dan dicari solusi permasalahan berupa nilai kedua variabel.
Sebagai contoh berikut adalah sistem pertidaksamaan linear dua variabel:
2x + 3y < 8
4x – 8y > 9
Banyaknya pertidaksamaan linear yang dibutuhkan untuk menemukan solusi pada sistem pertidaksamaan linear ditentukan oleh jumlah variabel atau peubahnya. Sebagai contoh pada sistem pertidaksamaan linear di atas adalah pertidaksamaan linear dua variabel sehingga dibutuhkan 2 pertidaksamaan juga.
Sementara pada sistem pertidaksamaan linear tiga variabel, maka dibutuhkan tiga pertidaksamaan linear juga untuk mendapatkan solusi atas semua variabelnya.
Contoh Soal Pertidaksamaan Linear
- Soal 1
Tentukan berapakah solusi dari pertidaksamaan linear yang ada di bawah ini untuk nilai variabel termasuk bilangan bulat positif atau bilangan cacah.

Jawab:
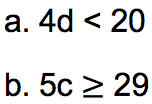
- Soal 2
Tentukan berapakah penyelesaian dari pertidaksamaan berikut ini:

Jawab:
a. a/2 < -1 (kedua ruas dikalikan dengan bilangan 2 agar tidak ada pecahan, tanda tidak berubah karena pengali positif)
a < -2
Apabila dibuat dalam bentuk grafik penyelesaian sebagai berikut:
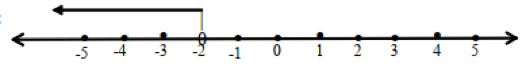
b. (kedua ruasnya dikalikan dengan angka 3 agar tidak ada pecahan)
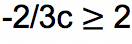
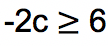
(kedua ruas dibagi dengan -2 yang menyebabkan tanda berubah menjadi sebaliknya)
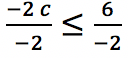
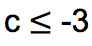
c. -2j + 10 > 4j – 2
2 + 10 > 4j + 2j (koefisien yang memiliki variabel dijadikan dalam satu ruas, dan konstanta di ruas satunya)
12 > 6j
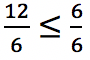
(kedua ruas dibagi dengan 6, tanda tidak berubah)
2 > j
- Soal 3
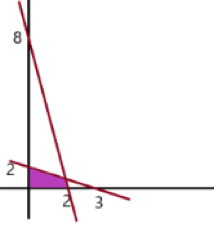
Tentukan penyelesaian sistem pertidaksamaan linear dua variabel dari:
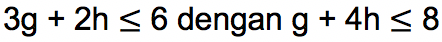
Jawab:
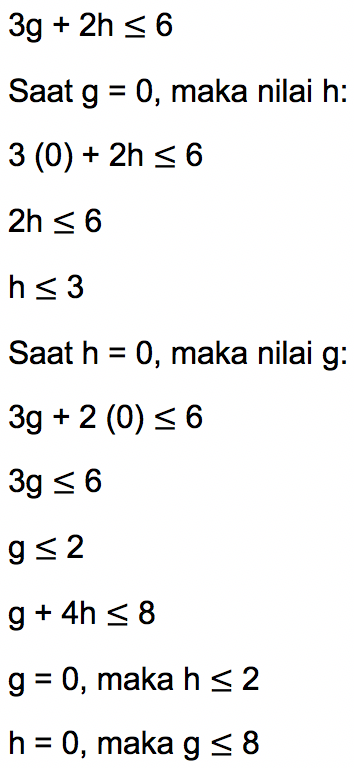
Jika digambar pada grafik diperoleh daerah penyelesaian pada area berwarna ungu.
Kesimpulan
Pertidaksamaan linear adalah bentuk kalimat terbuka yang mempunyai variabel dan kedua sisinya dihubungkan oleh tanda pertidaksamaan yakni:
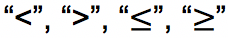
Bentuk pertidaksamaan linear dibedakan berdasarkan banyak variabel yang muncul, seperti pertidaksamaan satu variabel dan dua variabel.
