Dalam penulisan bilangan bulat pada Matematika, maka digunakanlah garis bilangan untuk menunjukkan posisi dari setiap bilangan-bilangan bulat tersebut. Bilangan bulat sendiri dibedakan menjadi beberapa klasifikasi seperti bilangan bulat positif, bilangan nol dan bilangan bulat negatif.
Pengertian Garis Bilangan
Garis bilangan adalah garis yang digunakan untuk menunjukkan dimana letak bilangan negatif, bilangan nol dan letak bilangan positif. Penulisan bilangan bulat yang meliputi bilangan bulat positif, nol dan negatif sangat lumrah menggunakan garis bilangan.
Pada buku Intisari Bimbel Terpadu, garis bilangan didefinisikan sebagai salah satu cara untuk merepresentasikan garis yang mana setiap titiknya mewakili bilangan-bilangan tertentu. Jarak setiap titik pada garis bilangan harus dibuat selalu sama.
Gambar 1 di bawah ini merupakan contoh aplikasi garis bilangan yang menunjukkan bilangan bulat positif, bilangan nol dan bilangan bulat negatif.
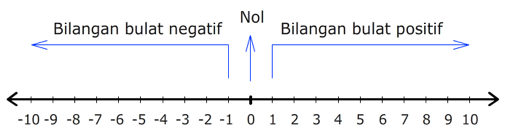
Penulisan bilangan bulat positif ada di sisi kanan dari bilangan nol yang diletakkan di tengah-tengah dan dimulai dari angka 1. Sementara bilangan bulat bernilai negatif ada di sisi kiri dari angka nol yang dimulai dari angka -1.
Bilangan yang dapat dibuat ke dalam garis bilangan meliputi bilangan rasional, bilangan real, hingga bilangan bulat termasuk di dalamnya adalah bilangan cacah dan bilangan asli.
Contoh Penerapan Garis Bilangan
Penggunaan garis bilangan mempunyai banyak fungsi dalam kehidupan terutama pada operasi hitung bilangan bulat. Garis bilangan dapat membantu para pelajar yang baru mempelajari konsep bilangan dan operasi hitung Matematika untuk lebih memahami mana nilai yang lebih besar dan lebih kecil.
Garis bilangan berfungsi untuk membandingkan dua bilangan yang bersifat negatif dan juga bilangan positif. Selanjutnya garis bilangan tersebut bisa digunakan untuk mengoperasikan bilangan bulat baik itu penjumlahan bilangan bulat positif dan negatif maupun pengurangan bilangan tersebut.
Cara Membuat Garis Bilangan
Agar garis bilangan yang dibuat lebih tepat maka harus mengikuti langkah-langkah berikut ini:
- Pertama-tama yang harus disiapkan untuk membuat garis bilangan yakni menggaris horizontal lurus sebagai tempat untuk membuat titik-titik
- Setelah garis lurus terbentuk, berikan titik-titik tepat pada garis tersebut untuk menempatkan bilangan pada garis bilangan. Pastikan bahwa jarak yang dibuat antara titik tersebut sama
- Setelah titik-titik pada garis bilangan dibuat, tuliskan bilangan di bawah titik tersebut. Untuk memudahkan penulisan, tempatkan bilangan nol terlebih dahulu pada garis bilangan sehingga dapat ditentukan di titik manakah yang merupakan bilangan positif dan bilangan negatif.
- Bilangan negatif dituliskan di sebelah kiri dari bilangan nol sementara bilangan positif diletakkan di sisi kanan dari bilangan nol. Semakin kanan bilangan maka semakin besar nilai bilangan tersebut sementara semakin kiri bilangan maka nilainya semakin kecil.
- Buat tanda panah di kedua ujung garisnya. Tanda panah berguna untuk menunjukkan bahwa bilangan akan terus berlanjut hingga tidak berhingga di kedua sisinya yakni sisi kanan yang semakin besar dan sisi kiri (Semakin kecil atau semakin negatif).
Cara Membaca Garis Bilangan
Ketika garis bilangan sudah dibuat, maka hal berikutnya yang harus dipahami adalah cara membaca garis bilangan. Apabila garis panah dengan ujung panahnya mengarah ke kiri, maka disebut sebagai “sebelum” dari angka di ujung garis panahnya.
Misalnya pada gambar di bawah ini menunjukkan garis bilangan yang mana suatu titik ada di bilangan positif 2. Selanjutnya dibuat tanda panah putus-putus yang mengarah ke sebelah kiri sebanyak 3 satuan sehingga ujung panahnya ada di atas angka -1.

Sehingga cara baca garis bilangan pada gambar di atas menjadi:
“Bilangan bulat 3 satuan yang terletak sebelum angka bilangan bulat positif 2 adalah -1”.
Operasi perhitungan penjumlahan pada bilangan bulat serta pengurangan juga bisa lebih mudah dipahami dengan menggunakan garis bilangan. Misalnya pada operasi perhitungan penjumlahan 8 + (-5) = …
- Langkah pertama pada garis bilangan ada tempatkan titik utama di bilangan 8 positif. Maju 8 langkah ke kanan dari angka 0 sebagai pusat pengamatan.
- Langkah kedua adalah penjumlahan yang pada hakikatnya akan menggerakkan panah ke arah kanan (Semakin besar) namun hal ini dipengaruhi juga oleh bilangan penjumlahnya.
- Bilangan 8 positif dijumlahkan oleh angka -5 atau negatif 5 sehingga arah panah dimundurkan 5 langkah ke kiri dari 8 positif.
- Hasil akhirnya tanda panah berhenti pada angka 3 atau bilangan 3 positif.
Operasi Hitung Menggunakan Garis Bilangan
Prinsip dalam operasi hitung bilangan bulat dengan garis bilangan sebagai berikut:
- Apabila bilangan bulat positif dijumlahkan dengan bilangan bulat positif, maka garis putus-putus dengan arah panah menuju ke kanan sehingga hasil tetap positif
- Apabila bilangan bulat positif dijumlahkan dengan bilangan bulat negatif, maka garis putus-putus dengan arah panah menuju ke kiri sehingga nilai bilangan berkurang. Apabila bilangan bulat positif lebih besar dibandingkan bilangan bulat negatif maka nilai bilangan tetap positif.
- Sementara jika bilangan bulat positif lebih kecil dibandingkan bilangan bulat negatif maka nilai bilangan akan menjadi negatif.
- Apabila bilangan bulat negatif dijumlahkan dengan bilangan bulat negatif, maka garis putus-putus dengan arah panah semakin menuju ke kiri sehingga lebih mengecil.
- Apabila bilangan bulat positif dikurangi dengan bilangan bulat positif, maka garis putus-putus dengan arah panah menuju ke kiri dengan jarak sesuai dengan bilangan bulat positif pengurangnya sehingga nilai bilangan menurun.
- Apabila bilangan bulat dikurangi dengan bilangan bulat negatif, maka garis putus-putus dengan arah panah menuju ke kanan dengan jarak sesuai dengan bilangan bulat negatif pengurangnya karena tanda kurang bertemu negatif menjadi positif (+). Misal: (-4) – (-3) = -4 + 3 = -1
Contoh Gambar Garis Bilangan
Pada Gambar 3 menunjukkan penjumlahan bilangan bulat menggunakan garis bilangan. Penjumlahan bilangan bulat positif dengan bilangan bulat positif maka garis putus-putus dengan arah panah menuju ke kanan (Semakin besar).
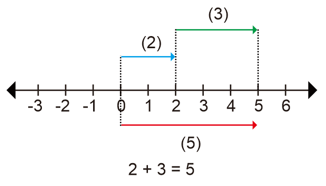
Contoh Soal Garis Bilangan
Hitunglah berapakah nilai operasi bilangan di bawah ini dengan menggunakan garis bilangan:
a. -5 + 6 =
b. 6 + (-4) =
Jawab:
a. -5 + 6 = 1
Jika dibuat pada garis bilangan, maka pertama-tama buat garis putus-putus dengan ujung panah di titik -5 atau negatif 5, selanjutnya karena ditambahkan dengan 6, arah panah menuju ke kanan sebanyak 6 langkah sehingga berhenti di titik 1 positif.
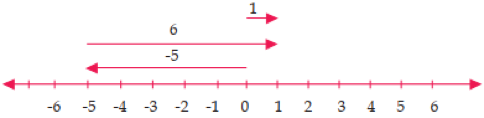
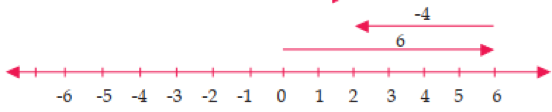
b. 6 + (-4) = 2
Pertama-tama dibuat garis putus-putus dengan ujung panah di titik 6, selanjutnya ditambahkan dengan -4, arah panah menuju ke kiri karena dijumlahkan dengan bilangan negatif sebanyak 4 langkah sehingga berhenti di titik 2 positif.
Kesimpulan
Garis bilangan bermanfaat dalam berbagai bidang di kehidupan terutama digunakan pada operasi hitung bilangan bulat. Garis bilangan dibuat secara mendatar atau horizontal yang mana angka nol ditempat di bagian tengah, angka yang bernilai positif di sisi kanan sementara bilangan bulat negatif di sisi kiri.
