Bilangan komposit adalah salah satu himpunan bilangan yang dipelajari secara mendalam di dalam materi Matematika. Bilangan komposit masuk ke dalam salah satu bagian bilangan asli. Sebagaimana bilangan lainnya dalam Matematika, bilangan ini digunakan untuk pengukuran dan pencacahan.
Pengertian Bilangan Komposit
Bilangan komposit adalah suatu himpunan bilangan dalam ilmu Matematika yang terdiri dari bilangan asli lebih dari 1 dan bukan termasuk bilangan prima. Bisa dikatakan pula bahwa bilangan komposit adalah bilangan cacah di luar bilangan 0 dan 1 serta selain bilangan prima.
Bilangan komposit juga disebut sebagai bilangan tersusun yang mempunyai faktor lebih dari dua. Bilangan komposit dihasilkan dari perkalian dua bilangan prima maupun lebih. Bisa dikatakan bahwa bilangan asli terdiri dari bilangan prima dan juga bilangan komposit.
Misal pada sepuluh bilangan komposit pertama terdiri dari 4, 6, 8, 9, 10, 12, 14, 15, 16, dan 18. Sementara bilangan prima terdiri dari 2, 3, 5, 7, 11, 13, 17, dan 19 yang merupakan angka di luar bilangan komposit.
Sebagai contoh 6 termasuk ke dalam bilangan komposit dikarenakan angka 6 bisa dibagi oleh angka 1, 2, 3 dan 6.
- Apabila angka 6 dibagi oleh 1 maka 6 : 1 = 6
- Apabila angka 6 dibagi oleh 2 maka 6 : 2 = 3 (Syarat komposit)
- Apabila angka 6 dibagi oleh 3 maka 6 : 3 = 2 (Syarat komposit)
- Apabila angka 6 dibagi oleh dirinya sendiri maka 6 : 6 = 1
Sehingga dapat dipahami bahwa angka 6 didapatkan dari perkalian dua bilangan prima yakni 2 x 3 = 6
Bilangan Komposit dari 1 Sampai 100
| 4 | 6 | 8 | 9 | 10 | 12 | 14 | 15 |
| 16 | 18 | 20 | 21 | 22 | 24 | 25 | 26 |
| 27 | 28 | 30 | 32 | 33 | 34 | 35 | 36 |
| 38 | 39 | 40 | 42 | 44 | 45 | 46 | 48 |
| 49 | 50 | 51 | 52 | 54 | 55 | 56 | 57 |
| 58 | 60 | 62 | 63 | 64 | 65 | 66 | 68 |
| 69 | 70 | 72 | 74 | 75 | 76 | 77 | 78 |
| 80 | 81 | 82 | 84 | 85 | 86 | 87 | 88 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 98 |
| 99 | 100 |
Harus dipahami bahwa bilangan 0 dan juga 1 tidak termasuk ke dalam bilangan prima dan juga bilangan komposit dikarenakan beberapa hal berikut ini:
- Angka 0 memiliki faktor tak terhingga serta tidak termasuk ke dalam himpunan bilangan asli
- Bilangan 1 hanya mempunyai sebanyak 1 faktor saja
- Oleh sebab itu bilangan komposit dimulai dari angka 4
Cara Mengenali Suatu Bilangan Komposit
Untuk mengetahui apakah suatu bilangan merupakan bilangan komposit atau bukan, bisa dicari tahu dengan cara mencari bilangan yang dapat membagi bilangan tersebut dengan sisa 0 atau tanpa sisa sama sekali. Lihat berapa banyak bilangan yang dapat membagi bilangan komposit.
Teorema yang berlaku dari bilangan komposit n dan bilangan prima p adalah:
- Suatu bilangan adalah bilangan prima apabila tidak ada bilangan prima p yang bisa membagi n dengan
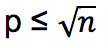
- Bilangan n adalah komposit jika terdapat bilangan prima p sehingga p | n dengan
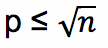
Jika faktor pembagi suatu bilangan lebih dari dua, maka bilangan tersebut adalah bilangan komposit. Berikut beberapa contoh untuk mengenali suatu angka merupakan bilangan komposit atau bukan:
- Angka 21 termasuk bilangan komposit karena bisa dibagi dengan angka 1, 3, 7, dan 21
Dibagi dengan angka 1 (21 : 1 = 21)
Dibagi dengan angka 3 (21 : 3 = 7)
Dibagi dengan angka 7 (21 : 7 = 3)
Dibagi dengan angka 21 (21 : 21 = 1)
- Angka 11 bukan termasuk bilangan komposit karena bilangan ini hanya bisa dibagi oleh 1 dan bilangan itu sendiri yakni 11
- Angka 2 x 2 x 2 atau 2^3 = 8 merupakan bilangan komposit karena melibatkan perkalian 2 bilangan prima atau lebih
Cara Menuliskan Himpunan Bilangan Komposit
Untuk menuliskan himpunan bilangan komposit sebenarnya tidak terdapat lambang khusus. Namun pada umumnya digunakan simbol huruf “K” untuk menunjukkan himpunan bilangan komposit.
- Himpunan bilangan komposit dengan nilai kurang dari 10
K = {4, 6, 8, 9}
Sehingga pada bilangan komposit kurang dari 10 terdapat 4 himpunan bilangan yaitu 4, 6, 8 dan 9
- Himpunan 10 bilangan komposit pertama
K = {4, 6, 8, 9, 10, 12, 14, 15, 16 dan 18}
- Himpunan bilangan komposit kurang dari 30
K = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, dan 28}
Sehingga terdapat 18 himpunan bilangan komposit yang kurang dari 30
Contoh Soal
- Tentukan apakah bilangan 157 merupakan bilangan prima atau komposit.
Jawab:
Untuk menentukan apakah bilangan 157 adalah bilangan prima atau komposit, maka harus dilihat dulu apakah ada bilangan prima yang bisa membagi 157. Caranya dengan mencari daftar bilangan prima ≤ akar 157 yaitu 2, 3, 5, 7 dan 11.
Bisa dilihat tidak ada satupun dari bilangan prima tersebut dapat membagi 157 hingga tanpa sisa. Sehingga 157 adalah bilangan prima.
- Tentukan apakah bilangan 221 merupakan bilangan prima atau komposit.
Jawab:
Sama seperti pada nomor 1, untuk menentukan apakah bilangan 221 adalah bilangan prima atau komposit, maka harus dilihat dulu apakah ada bilangan prima yang bisa membagi 221. Caranya dengan mencari daftar bilangan prima
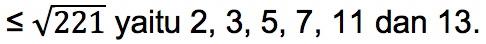
Bisa dihitung bahwa 221 dapat dibagi oleh 13 dan menghasilkan bilangan 17. Sehingga dapat disimpulkan bahwa 221 merupakan bilangan komposit.
- Tentukan apakah bilangan 177 merupakan bilangan prima atau komposit.
Jawab:
Untuk menentukan apakah bilangan 177 adalah bilangan prima atau komposit, maka harus dilihat dulu apakah ada bilangan prima yang bisa membagi 177. Caranya dengan mencari daftar bilangan prima
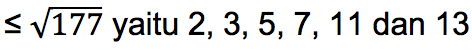
Bisa dihitung bahwa 221 dapat dibagi oleh 3 dan menghasilkan bilangan 59. Sehingga dapat disimpulkan bahwa 221 merupakan bilangan komposit.
- Tentukan apakah bilangan 167 merupakan bilangan prima atau komposit.
Jawab:
Untuk menentukan apakah bilangan 167 adalah bilangan prima atau komposit, maka harus dilihat dulu apakah ada bilangan prima yang bisa membagi 167. Caranya dengan mencari daftar bilangan prima
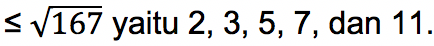
Bisa dilihat tidak ada satupun dari bilangan prima tersebut dapat membagi 167 hingga tanpa sisa. Sehingga 167 adalah bilangan prima.
Dalam materi Matematika, bilangan adalah suatu konsep yang digunakan untuk pengukuran dan pencacahan sehingga dapat menyatakan jumlah dan banyak sesuatu. Bilangan komposit merupakan salah satu bagian bilangan asli yang bukan termasuk bilangan prima.
