Bilangan Rasional & Irasional: Pengertian, Contoh Soal

Konsep bilangan rasional irasional penting untuk dipelajari karena merupakan dasar bagi berbagai operasi Matematika seperti bentuk akar dan juga perubahan bilangan bentuk akar menjadi bilangan berpangkat. Bilangan rasional dan irasional terdiri dari berbagai bilangan seperti bilangan bulat dan lainnya.

Pengertian Bilangan Rasional

Konsep bilangan rasional irasional mendasari perhitungan bilangan bentuk akar yang merupakan kebalikan dari pemangkatan suatu bilangan. Bilangan real terdiri dari gabungan antara bilangan rasional dan irasional.

Bilangan rasional sendiri adalah bilangan real yang dituliskan sebagai perbandingan antara dua bilangan bulat a dan b, bisa dituliskan sebagai a/b dengan nilai b tidak boleh sama dengan 0. Batasan pada bilangan rasional meliputi -∞, ∞.

Bilangan rasional apabila ditulis sebagai pecahan desimal akan membentuk pola bilangan tertentu apabila angkanya tidak berhenti atau bisa juga angkanya berhenti di suatu nilai.

Bilangan rasional terdiri dari bilangan pecahan biasa, bilangan bulat, bilangan cacah serta bilangan pecahan campuran. Bilangan rasional bisa ditulis sebagai bilangan desimal dengan deret angka berulang teratur, seperti 0,25000… (angka 0 berulang teratur).

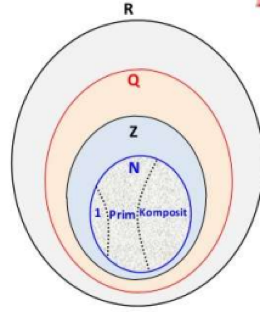
Keterangan:

R = Himpunan bilangan real
Q = Himpunan bilangan rasional
Z = Himpunan bilangan bulat
N = Himpunan bilangan asli

Terlihat pada Gambar 1 di atas bahwa bilangan rasional termasuk ke dalam bilangan real yang terdiri dari bilangan bulat dan bilangan asli.

Contoh Bilangan Rasional

Bilangan rasional terdiri dari bilangan rasional pecahan biasa atau disebut sebagai pecahan biasa seperti ½, ¾ , 2/5, 3/5, 5/8, …, a/b. Pecahan biasa merupakan pecahan yang mempunyai nilai penyebut lebih besar dibandingkan nilai pembilangnya.

Pada pecahan a/b, bilangan a disebut pembilang dan b adalah penyebut. Bilangan rasional lainnya adalah bilangan rasional pecahan sempurna atau yang biasa disebut sebagai pecahan campuran. Bilangan pecahan campuran yang merupakan bilangan rasional adalah 2 ½, 75/6, 25/8, 26/4 dan seterusnya. 

Bilangan rasional apabila ditulis sebagai bilangan desimal maka ditulis dengan deret angka berulang teratur. Berikut beberapa contoh bilangan rasional deret angka berulang teratur:

1/8 = 0,125000… (angka 0 berulang teratur)

2/3 = 0,6666… (angka 6 berulang teratur)

3/7 = 0,428571428571… (angka 428571 berulang teratur)

17/9 = 1,8888… (angka 8 berulang teratur)

3/2 = 1,5000… (angka 0 berulang teratur)

Pengertian Bilangan Irasional

Bilangan irasional merupakan bilangan real yang mengandung pecahan desimal tidak berhingga dan tidak berpola. Bilangan irasional adalah bilangan real yang tidak termasuk bilangan rasional. Bilangan irasional bukan termasuk bilangan bulat serta juga bukan merupakan bilangan pecahan.

Bilangan irasional yang memakai tanda akar (√) disebut bentuk akar. Namun, tidak seluruh bilangan yang ada di dalam tanda akar termasuk ke dalam bilangan irasional.

Hal ini karena beberapa bilangan di dalam tanda akar dapat ditarik akarnya menjadi bilangan bulat tertentu ataupun bilangan desimal berhingga dan berpola.

Misalnya bilangan √25 bernilai 5 dan √36 bernilai 6 bukan merupakan bilangan irasional, namun bilangan rasional. Contoh bentuk akar bilangan irasional adalah √20 dan √18 karena nilainya tidak berhingga dan tidak berpola. Sama seperti batasan pada bilangan rasional, batasan bilangan irasional meliputi -∞, ∞.

Contoh Bilangan Irasional

Contoh bilangan irasional adalah pada akar 2, yakni √2 = 1,414213562373…. Nilai akar 2 apabila dihitung tidak akan pernah ada habisnya dan juga tidak mempunyai pola tertentu. Kemudian ada juga bilangan euler (e) yang termasuk bilangan irasional karena memiliki nilai e = 2,718281828… (dan seterusnya).

Nilai phi (π) yang merupakan konstanta untuk perhitungan luas dan keliling lingkaran juga bilangan irasional yakni 22/7 yang apabila dihitung menjadi bilangan desimal bernilai 3,141592653…. (dan seterusnya tanpa ada akhirnya).

Bilangan Rasional Irasional dalam Kehidupan Sehari-Hari

Bilangan rasional irasional memiliki aplikasi yang sangat luas dalam kehidupan sehari-hari. Hal ini karena bilangan rasional dan irasional merupakan penyusun bilangan real yang merupakan himpunan bilangan nyata atau asli yang terdiri dari angka hitung bersifat natural.

Bilangan rasional irasional digunakan dalam perhitungan matematika, geometri, ekonomi, fisika dan sebagainya.

Operasi Perhitungan Bilangan Rasional Irasional

1. Operasi Penjumlahan

Operasi penjumlahan pada bilangan rasional dan irasional adalah operasi untuk menjumlahkan angka-angka yang ada. Untuk memudahkan operasi penjumlahan pada bilangan rasional dan irasional, maka bentuk bilangan harus disamakan terlebih dahulu.

Misalnya, penjumlahan bilangan berbentuk pecahan dengan pecahan desimal harus disamakan bentuknya ke bentuk desimal atau pecahan. Contoh:

0,5 + 3/7 (pecahan 3/7 diubah ke bentuk desimal)
= 0,5 + 0,43
= 0,93

Pecahan 3/7 dijadikan pecahan desimal dan kemudian dibulatkan dua angka di belakang koma.

Operasi penjumlahan dan perkalian bilangan rasional irasional bersifat komutatif dan asosiatif. Sifat komutatif yakni sifat pertukaran yang mana operasi penjumlahan dan perkalian akan menghasilkan nilai  yang sama meskipun posisi bilangan ditukar.

Misalnya, penjumlahan 24 + 16 = 16 + 24 = 40 (sifat komutatif). Sementara perkalian juga bersifat komutatif seperti 3 x 5 = 5 x 3 = 15 (sifat komutatif)

Sementara sifat asosiatif atau pengelompokan adalah mengelompokkan beberapa bilangan pada perkalian atau penjumlahan tiga bilangan atau lebih dengan tanda kurung (). Misal:

(5 x 4) x 2 = 5 x (4 x 2)  (sifat asosiatif)
20 x 2 = 5 x 8
40 = 40

2. Operasi Pengurangan dan Pembagian

Operasi pengurangan dan pembagian bilangan rasional irasional seperti halnya operasi pengurangan bilangan bulat. Pada operasi bilangan rasional dan irasional tidak berlaku sifat komutatif dan asosiatif. Posisi bilangan mempengaruhi hasil operasi yang diperoleh.

3. Aturan Pembulatan Angka

Bilangan rasional irasional melibatkan pembulatan angka karena di dalamnya terdapat bilangan pecahan dan pecahan desimal. Pembulatan angka dilakukan untuk menyederhanakan beberapa angka di belakang koma yang panjang terutama bilangan irasional dengan angka di belakang koma tidak pernah berhenti.

Berikut adalah beberapa aturan pembulatan angka:

• Apabila angka desimal lebih besar dari 5 maka angka di depannya dibulatkan ke atas
• Apabila angka desimal kurang dari 5 maka angka di depannya bernilai tetap. Misalnya 0,36 dibulatkan satu angka di belakang koma menjadi 0,4 karena 6 lebih besar dari 5 sehingga 3 dibulatkan ke atas

Contoh Soal Bilangan Rasional Irasional

Tentukan dari bilangan-bilangan di bawah ini mana yang merupakan bilangan rasional dan irasional.

a. 1/3
b. 3/17
c. ½
d. 2/5

Kesimpulan

Mempelajari konsep bilangan rasional irasional sangat penting dan harus dipahami oleh pelajar sebelum mempelajari operasi Matematika lainnya seperti bentuk akar dan perubahan bentuk akar menjadi bilangan pecahan. Baik bilangan rasional dan irasional keduanya termasuk ke dalam bilangan real.