Bilangan Kompleks: Pengertian, Operasi, Contoh Soal

Bilangan kompleks adalah bilangan yang mungkin cukup asing bagi sebagian orang. Bilangan kompleks terdiri dari bilangan real yang biasa digunakan pada kehidupan sehari-hari dan bilangan imajiner yang hanya diterapkan pada sebagian bidang saja.

Pengertian Bilangan Kompleks

Bilangan kompleks terdiri dari penjumlahan atau pengurangan bilangan real dan bilangan imajiner yang ditandai dengan notasi j.

Bilangan kompleks = (bilangan real) + j (bagian imajiner)

Sebagai contoh penulisan bilangan kompleks adalah 5 + j3 yang mana angka 5 adalah bagian real sementara 3 adalah bagian imajinernya. Penjelasan mengenai bilangan riil dan bilangan imajiner akan dijelaskan pada bagian di bawah ini.

Grafik Bilangan Kompleks

Bilangan kompleks yang dituliskan dengan y = a + bj bisa disingkat dengan pasangan terurut (a, b). Sehingga bilangan kompleks juga dapat dituliskan dalam sebuah bidang datar seperti koordinat titik pada sistem koordinat kartesius.

Bidang kompleks atau bidang Argand adalah bidang yang digunakan untuk menggambarkan bilangan kompleks.

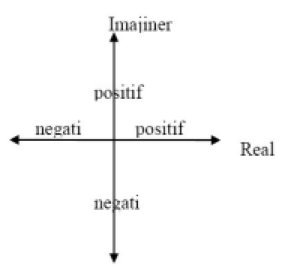
Sehingga apabila terdapat bilangan kompleks y = 4 + 6j, angka 4 adalah bilangan real positif terletak di kuadran I sementara 6 adalah bilangan imajiner positif. Jika dibuat grafiknya akan seperti Gambar 3 di bawah ini.

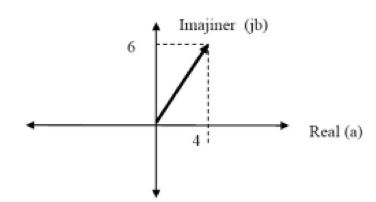
Seperti halnya koordinat Kartesius, grafik bidang kompleks juga dibagi berdasarkan daerahnya atau kuadrannya. Kuadran pada bidang kompleks dibagi menjadi empat kuadran berdasarkan letak posisi sudutnya.

• Kuadran I ada pada sudut 0 sampai dengan 90⁰
• Kuadran II ada pada sudut 90⁰ sampai dengan 180⁰
• Kuadran III ada pada sudut 180⁰ sampai dengan 270⁰
• Kuadran IV ada pada sudut 270⁰ sampai dengan 360⁰

Contoh Penerapan Bilangan Kompleks

Penerapan bilangan kompleks banyak digunakan di kehidupan sehari-hari seperti di bidang teknik fisika. Ada banyak penerapan bilangan kompleks pada bidang fisika modern seperti mekanika kuantum. Selain itu bilangan kompleks juga bermanfaat dalam bidang pemrosesan digital.  

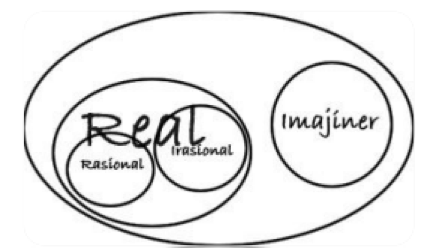
Bilangan Riil

Bilangan riil merupakan sistem bilangan yang biasa digunakan dalam aktivitas sehari-hari. Bilangan riil terdiri dari bilangan rasional dan bilangan tidak rasional atau irasional. Bilangan riil disimbolkan dengan notasi R yang mana di dalamnya termasuk bilangan bulat, bilangan asli, bilangan pecahan dan sebagainya.

Bilangan Imajiner

Bilangan imajiner bisa dikatakan adalah bilangan yang nilainya secara teoritis tidak ada karena merupakan akar kuadrat dari sebuah bilangan bernilai negatif. Sebagai contoh bilangan imajiner adalah √-2, √-3, dan √-4.

Secara teoritis bilangan negatif tidak mungkin ada nilai akar kuadratnya karena tidak ada bilangan yang apabila dipangkatkan dua bernilai negatif. Misalnya bilangan 2 dan -2 apabila dipangkatkan kuadrat akan bernilai 4 positif.

Oleh karena itu √-a tidak bisa dituliskan dengan bilangan biasa, karena tidak ada bilangan real yang memenuhi bilangan tersebut. Bilangan imajiner bisa dituliskan dengan:

-a = -1 x a

Misalnya:

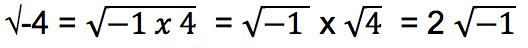
Bilangan √-1 masih tidak bisa dioperasikan seperti halnya bilangan real karena merupakan bilangan imajiner. Oleh karena itu bilangan √-1 bisa dinotasikan dengan “j” sehingga pada bilangan imajiner 2√-1 bisa dinotasikan dengan j2.

Dengan menggunakan notasi pengganti berupa huruf “j” maka penulisan akan lebih rapi.

Operasi Bilangan Kompleks

1. Operasi Penjumlahan dan Operasi Pengurangan

Operasi penjumlahan dan operasi pengurangan pada bilangan kompleks seperti halnya operasi penjumlahan dan pengurangan aljabar. Caranya adalah dengan mengoperasikan bilangan yang sama-sama real kemudian bagian yang sama-sama imajiner dijumlahkan atau dikurangkan dengan sesamanya.

Contoh:

Penjumlahan (3 – j2) + (4 + j5)
= (3 + 4) + j (-2 + 5)
= 7 + j3

Pengurangan (3 – j2) – (4 + j5)
= 3 – j2 – 4 – j5
= (3 – 4) + j (– 2 – 5)
= -1 – j7

Secara umum pada penjumlahan dan pengurangan berlaku formula berikut ini:

(g + jh) + (i + jk) = (g + i) + j (h + k)
(g + jh) – (i + jk) = (g – i) + j (h – k)

2. Operasi Perkalian

Operasi perkalian pada bilangan kompleks memiliki sifat distributif perkalian seperti halnya pada bilangan real. Apabila faktor yang dikalikan ada lebih dari dua faktor, maka setiap faktor dikali secara bertahap.

(2 – j5) (1 – j2) (3 + j4)

= (2 – j4 – j5 + j²10) (3 + j4)

= (2 – j9 – 10) (3 + j4)

= (-8 – j9) (3 + j4)

= (-24 – j24 – j27 – j²36)

= (-24 – j51 + 36) (ingat: j² = -1)

= (12 – j51)

Pada kasus khusus, perkalian bilangan kompleks tidak menghasilkan suku j atau menghasilkan bilangan real. Perkalian bilangan kompleks yang menghasilkan bilangan real disebut sebagai bilangan konjugat.

Dua bilangan kompleks konjugat yang dikali akan selalu menghasilkan bilangan real. Berikut persamaannya:

Bilangan kompleks konjugat: (c + d) (c – d) = c² – d²

Contoh:

(6 – j8) (6 + j8)

= 36 – (j8)²

= 36 – j²8²

= 36 + 8² (j² = -1)

= 36 + 64

= 100

3. Operasi Pembagian

Pembagian bilangan kompleks baru dapat dilakukan apabila penyebutnya berupa bilangan real. Oleh karena itu apabila persoalan pembagian bilangan kompleks memiliki penyebut bilangan kompleks, penyebutnya harus dikali menjadi bilangan kompleks konjugatnya agar berubah menjadi bilangan real.

Contoh:

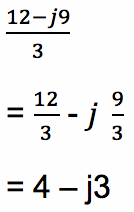
Sementara jika penyebutnya merupakan bilangan kompleks, maka harus dikali dengan konjugatnya agar menjadi bilangan real.

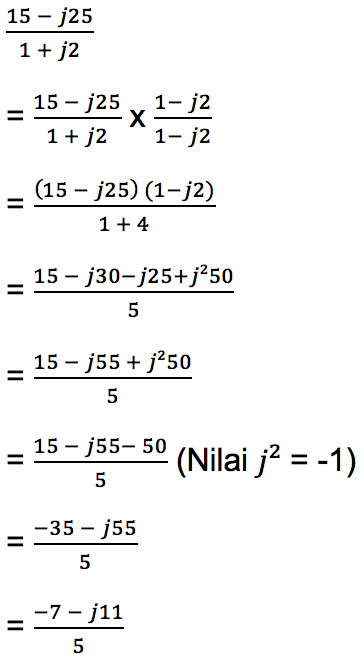
Contoh Soal Bilangan Kompleks

• Soal 1

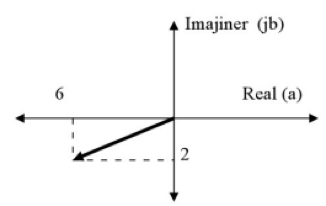
Buatlah ke dalam bentuk grafik dari bilangan kompleks y = -6 – j2

Pembahasan

Jawab:

Angka -6 adalah bilangan real negatif sementara -2 adalah bilangan imajiner negatif sehingga terletak di kuadran III. Jika dibuat grafiknya akan seperti gambar  di bawah ini.

• Soal 2

Tentukan berapa hasil penjumlahan dan pengurangan dari bilangan di bawah ini

x1 = 5 + j4 dan x2 = 2 – j3

a. x1 + x2
b. x1 – x2

Kesimpulan

Bilangan kompleks terdiri dari bilangan real dan bilangan imajiner yang dihubungkan dengan notasi positif (+) dan negatif (-). Bilangan kompleks banyak digunakan di kehidupan sehari-hari seperti di bidang teknik fisika dan digital.