Skala Peta: Pengertian, Manfaat, Cara Menghitung, Soal

Salah satu komponen penting pada peta ataupun sketsa bangunan yang wajib disertakan adalah skala peta. Skala merupakan aplikasi perbandingan ukuran yang menunjukkan berapa besar sebuah gambar dibandingkan benda aslinya.

Pengertian Skala Peta

Skala peta merupakan perbandingan ukuran yang menunjukkan perbandingan antara ukuran pada denah atau peta dengan ukuran objek yang sebenarnya. Antara perbandingan, skala dan juga pecahan memiliki relasi yang erat karena terdapat notasi atau tanda yang sama yakni tanda bagi (:).

Penulisan skala peta selalu berada di sudut bawah peta yang tertulis kata skala dan disertai oleh angka sebagai perbandingan. Misalnya sebuah peta yang memiliki skala sebesar 1 : 900, artinya setiap 1 cm pada peta maka nilainya sama dengan 900 cm atau 9 meter untuk ukuran sebenarnya.

Skala umumnya ditetapkan menggunakan ukuran cm sehingga setiap 1 cm pada peta nilainya sama dengan nilai pembanding skala yang sudah ditetapkan. Misalnya pada skala 1 : 3.500.000, menunjukkan bahwa setiap 1 cm sama dengan 3.500.000 cm yang jika diubah dalam km menjadi 35 km.

Sehingga setiap 1 cm pada peta memiliki jarak 35 km yang sebenarnya. Penggunaan skala bermanfaat dalam memudahkan pengguna untuk menghitung atau memperkirakan jarak asli dan ukuran asli dari benda melalui gambar denah dan peta yang ada.

Pemanfaatan Skala Pada Kehidupan

Penerapan skala peta mempunyai manfaat yang sangat luas dalam kehidupan sehari-hari. Skala banyak digunakan oleh para arsitek atau perancang bangunan saat membangun gedung, rumah, taman dan sebagainya.

Pada pembuatan sebuah miniature bangunan, taman, hingga miniatur benda seperti prototype dan lainnya juga menerapkan skala untuk menunjukkan perbandingan antara miniatur benda dengan rancangan benda aslinya.

Rumus Skala

Rumus skala diturunkan dari pengertian skala yang merupakan perbandingan antara ukuran pada peta atau denah dengan ukuran yang sebenarnya. Berikut adalah rumus untuk mencari skala:

Skala = ukuran pada peta/ukuran yang sebenarnya

Sehingga dari rumus di atas bisa dihitung ukuran pada peta dan ukuran sebenarnya apabila informasi yang diketahui adalah skala.

Ukuran pada peta = skala x ukuran yang sebenarnya
Ukuran yang sebenarnya = ukuran pada peta/skala

Contoh Soal Skala Peta

• Soal 1

Sebuah denah untuk taman belakang rumah memiliki lebar sebesar 10 cm dengan panjang sebesar 12 cm. Skala yang ditunjukkan pada denah taman belakang rumah adalah 1 : 150. Tentukan berapa lebar dan juga panjang ukuran sebenarnya dari taman belakang rumah tersebut.

Pembahasan

Diketahui:

p1 = 12 cm
l1 = 10 cm
Skala = 1 : 150

Ditanya:

Panjang (p2) dan lebar (l2) sebenarnya.

Jawab:

Diketahui bahwa pada skala dengan perbandingan angka 1 : 150, menunjukkan bahwa 1 cm pada denah tersebut sama ukurannya dengan 150 cm taman belakang rumah yang sebenarnya. Sehingga untuk mengukur panjang dan lebar sebenarnya dengan rumus berikut:

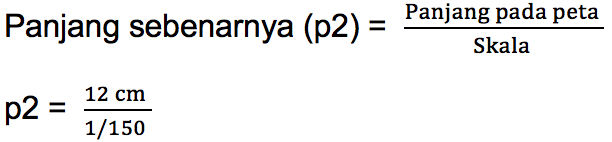
p2 = 12 x 150
p2 = 1800 cm atau 18 m

Sehingga panjang sebenarnya dari taman belakang rumah sebesar 18 m

l2 = 10 x 150 
l2 = 1500 cm atau 15 m

Sehingga lebar sebenarnya dari taman belakang rumah sebesar 15 m

• Soal 2

Sebuah menara pemancar telekomunikasi dibangun di lapangan kosong luas yang ada di pinggir desa. Sebuah denah dibuat untuk menggambarkan posisi menara pemancar telekomunikasi tersebut yang memiliki skala 1 : 1000.

Pada denah tampak bahwa tinggi menara telekomunikasi sebesar 13 cm dan panjang bayangan sebesar 9 cm. Tentukan:

a. Panjang bayangan menara telekomunikasi yang sebenarnya (p2)
b. Tinggi menara telekomunikasi yang sebenarnya (t2)

Pembahasan

Jawab:

a. Panjang bayangan menara pada denah adalah sebesar 9 cm dengan skala 1 : 1000. Maka panjang bayangan menara sebenarnya adalah:

b. Tinggi menara telekomunikasi pada denah adalah sebesar 13 cm dengan skala 1 : 1000. Maka tinggi menara sebenarnya adalah:

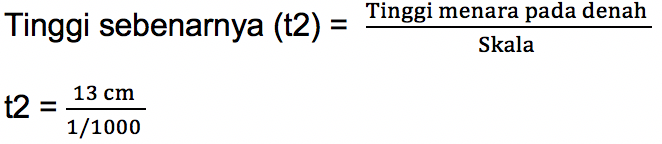
t2 = 13 x 1000
t2 = 13000 = 130 meter

Maka panjang bayangan menara sebenarnya adalah 90 meter dengan tinggi menara sebenarnya adalah 130 meter.

• Soal 3

Jarak kota Yudi dan Bambang yang tampak di peta adalah 50 cm. Jarak sebenarnya kota Yudi dan Bambang adalah sebesar 600 km. Tentukan berapakah skala yang harus dituliskan pada peta tersebut.

• Soal 4

Diketahui sebuah atlas menunjukkan skala sebesar 1 : 3.000.000 di bagian bawah sudut atlas. Setelah diukur pada atlas, didapat jarak dari kota S ke kota D sepanjang 5 cm. Tentukan berapa kilometer jarak antara kota S ke kota D yang sebenarnya?

Pembahasan

Diketahui:

skala = 1 : 3.000.000
jarak peta = 5 cm

Ditanya:

Jarak sebenarnya?

Jawab:

Untuk menghitung jarak sebenarnya antara kota S ke kota D bisa menggunakan rumus berikut:

Ukuran yang sebenarnya = ukuran pada peta/skala

Ukuran yang sebenarnya = 5 cm x 3.000.000

Ukuran yang sebenarnya = 15.000.0000 cm diubah ke satuan km sehingga 15.000.000 : 100.000 = 150 km

• Soal 5

Seorang arsitektur akan membuat lapangan dengan bentuk lingkaran yang memiliki jari-jari sebesar 21 cm. Apabila arsitektur tersebut membuat skala pada denah lapangan sebesar 1 : 1000, tentukan berapa luas lapangan yang sedang dirancang oleh arsitektur?

Pembahasan

Diketahui:

r = 21 cm (lingkaran pada gambar)
skala = 1 : 1000

Ditanya:

Luas lapangan yang sebenarnya dirancang arsitektur (L)?

Jawab:

Untuk menghitung luas lapangan yang sebenarnya bisa dengan menghitung jari-jari lapangan yang sebenarnya terlebih dulu.

Jari-Jari yang sebenarnya = 21.000 cm atau diubah ke m menjadi 210 m

Luas lapangan = 22/7 x 210 x 210 = 138.600 m²

Kesimpulan

Skala peta merupakan perbandingan ukuran yang menunjukkan berapa besar jarak pada gambar dibandingkan jarak aslinya. Aplikasi skala peta sangat banyak di kehidupan sehari-hari. Skala peta banyak dimanfaatkan oleh arsitektur dalam merancang denah bangunan, taman, lapangan dan sebagainya.