Materi mengenai limit fungsi sangat penting sebagai dasar dalam mempelajari teorema kalkulus. Konsep limit sendiri diperkenalkan oleh Agustin Louis Cauchy di abad ke 18 untuk membantu para ilmuwan dalam menghitung nilai-nilai fungsi yang ada di sekitar titik yang akan dihitung.
Pengertian Limit Fungsi
Limit fungsi bisa didefinisikan sebagai kondisi dimana nilai fungsi bergerak mendekati suatu nilai tertentu atau menuju suatu batasan nilai tertentu, namun nilai tersebut tidak dapat dicapai.
Limit fungsi dituliskan menggunakan notasi sebagai berikut:
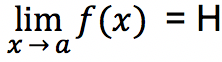
Arti persamaan limit fungsi di atas adalah untuk setiap nilai x yang mendekati dengan nilai a namun nilai x tidak sama dengan a, maka nilai f(x) mendekati H. Semakin dekat nilai x ke a, maka semakin dekat pula f(x) ke H.
Rumus Limit Fungsi
Untuk mengerjakan soal berkaitan dengan limit fungsi, maka hal pertama yang harus dikuasai adalah pengetahuan mengenai sifat-sifat limit fungsi. Jika k adalah konstanta, f dan h adalah fungsi yang memiliki limit di x → b, b ϵ R, maka berlaku padanya sifat limit fungsi berikut:
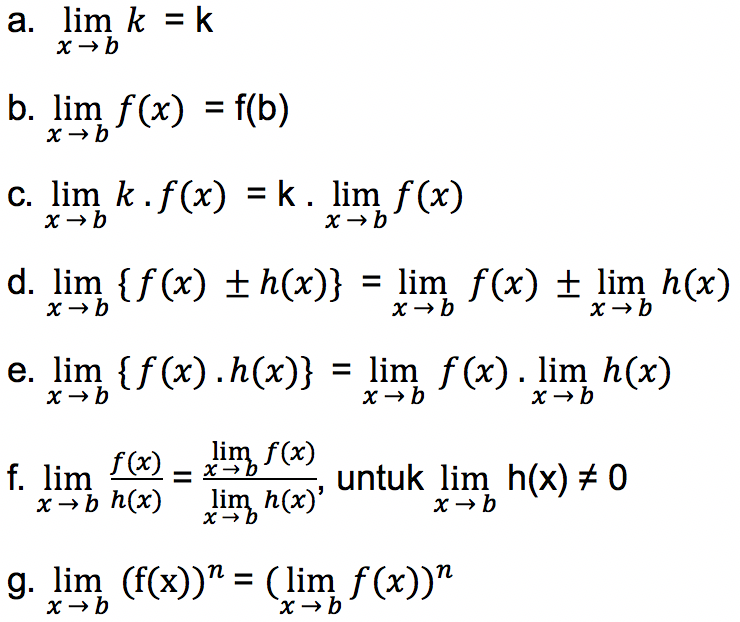
Limit Fungsi Aljabar
Limit f(x) dengan nilai x mendekati b sama dengan Y, maka dituliskan sebagai:
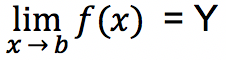
Apabila bisa dibuat nilai f(x) sembarang yang nilainya dekat dengan Y (paling dekat sesuai dengan yang diinginkan) dengan cara mengambil nilai x yang mendekati b, namun nilai x tersebut tidak sama dengan b.
Secara sederhana, dapat digambarkan sebagai nilai fungsi f(x) akan semakin mendekati nilai Y apabila nilai x mendekati nilai b (dari kedua sisinya baik positif dan negatif) namun nilai x tidak sama dengan b. Notasi limit
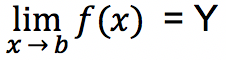
juga bisa dituliskan dengan:
f(x) → Y seraya x → b
Contoh Soal Limit Fungsi Aljabar & Pembahasan
- Soal 1
Diketahui dua buah fungsi memiliki persamaan sebagai berikut:
Fungsi f (x) = 15x + 7 dan fungsi g (x) = 2x² + 8x – 7. Tentukan berapakah nilai pada:
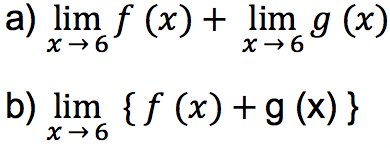
Jawab:
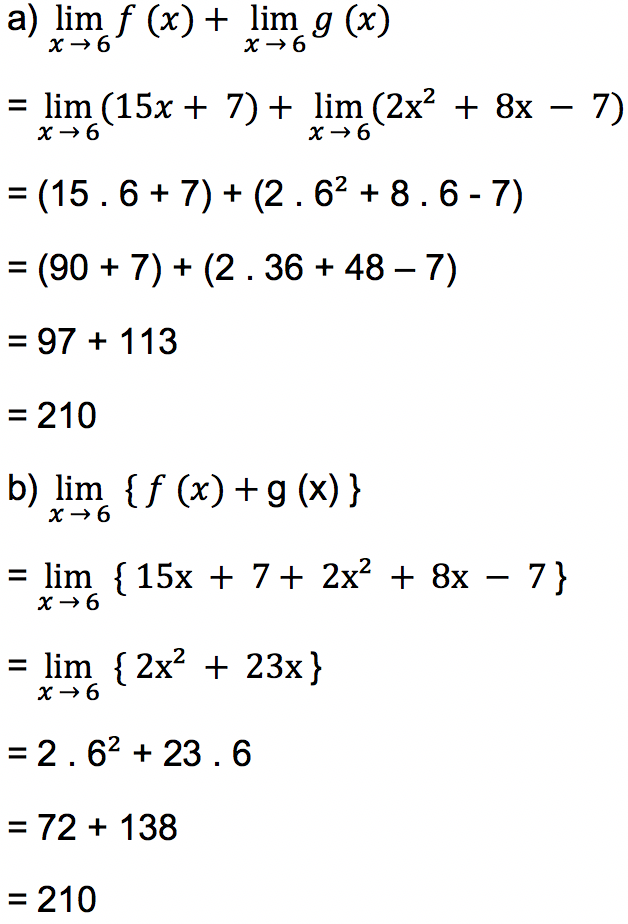
- Soal 2
Tentukan nilai limit dari fungsi di bawah ini:
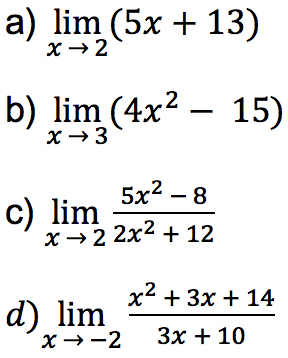
Jawab:
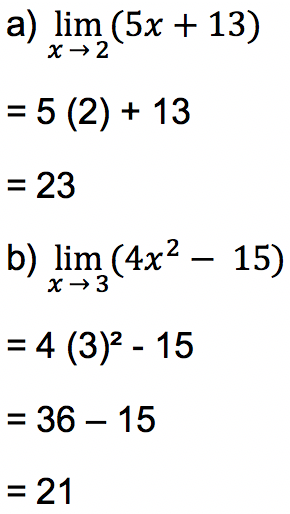
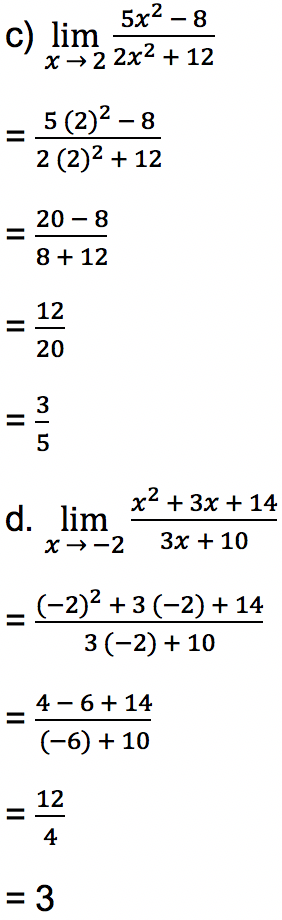
Limit Fungsi Tak Hingga
Untuk memahami konsep limit fungsi tak hingga, dapat dimisalkan sebuah fungsi f(x) = 3/x. Jika nilai variabel x semakin besar, maka nilai fungsi f(x) justru akan semakin mengecil. Jika nilai variabel x sangat besar atau bahkan mendekati tidak terhingga, maka nilai variabel x dituliskan dengan x → ∞.
Sehingga untuk fungsi f(x) = 3/x pada x → ∞, maka nilainya akan semakin mendekati nol. Kesimpulannya adalah limit dari 3/x untuk variabel x mendekati tidak berhingga adalah 0. Berikut rumus limit fungsi tak berhingga:
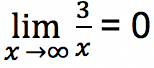
Limit fungsi yang memiliki bentuk
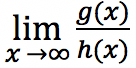
bisa dikerjakan dengan cara melakukan pembagian pembilang g(x) dengan penyebutnya h(x). Syaratnya adalah penyebut h(x) memiliki xn dengan n merupakan pangkat paling besar dari pembilangnya g(x).
Apabila bentuk limit fungsi pada variabel x memiliki pangkat xn dengan n lebih besar pada bagian penyebut dibanding pembilang, maka hasil limit fungsinya adalah 0 seperti di bawah ini:
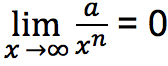
Contoh Soal Limit Fungsi Tak Hingga & Pembahasan
- Soal 1
Tentukan berapakah nilai limit fungsi tak hingga dari persamaan berikut
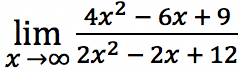
Jawab:
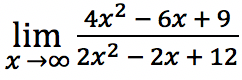
Untuk mengerjakan soal limit fungsi tak hingga di atas, pertama-tama pembilang dan juga penyebut bilangan dibagi oleh x²
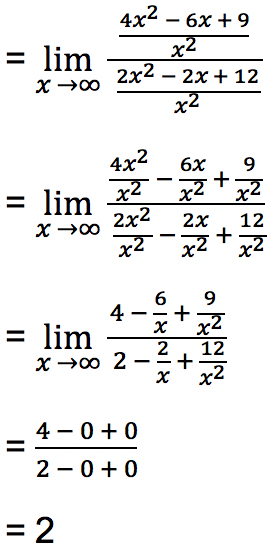
- Soal 2
Tentukan berapakah nilai limit fungsi tak hingga dari persamaan berikut
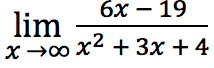
Jawab:
Sama seperti soal nomor 1, pertama-tama penyebut dan pembilang dibagi dengan x².
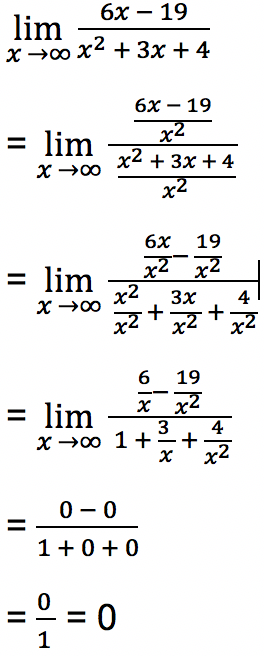
Baca Juga : Kumpulan Contoh Soal Limit & Pembahasannya
Untuk dapat mengerjakan soal berbentuk limit fungsi, maka kemampuan yang harus dikuasai adalah pemahaman terhadap sifat limit fungsi aljabar dan limit fungsi di tak terhingga. Agar lebih lancar dalam penguasaan soal limit, maka harus lebih sering berlatih bentuk-bentuk soalnya.
