Kubus adalah salah satu jenis bangun ruang yang sangat mudah dijumpai dalam kehidupan sehari-hari. Sisi pada bangun ruang kubus berbentuk persegi yang sama panjang (kongruen). Kubus termasuk ke dalam bangun ruang sisi datar karena semua sisinya mendatar dan tidak melengkung.

Daftar Isi show

Pengertian Kubus

Kubus merupakan bangun ruang tiga dimensi yang mempunyai panjang, lebar dan tinggi sehingga terdapat aspek “kedalaman” atau volume. Bangun kubus memiliki sisi berbentuk bidang datar persegi dengan ukuran semua sisi pada kubus sama panjang.

Bangun ruang kubus mempunyai 3 unsur utama pembentuknya yakni unsur sisi, rusuk serta titik sudut. Rusuk yaitu garis yang dibentuk oleh perpotongan dari sisi pada bangun ruang. Kubus punya 12 rusuk dengan ukuran sama panjang. Rusuk kubus terdiri dari rusuk bersilangan, rusuk sejajar dan berpotongan.

Bangun kubus diberi nama berdasarkan nama-nama setiap titik sudutnya yakni pada sisi alas dan juga sisi atas kubus. Sebagai contoh pada gambar di bawah ini maka bangun kubus tersebut diberi nama sebagai kubus ABCD.EFGH dimana bidang ABCD adalah alas dan bidang EFGH adalah atasnya.

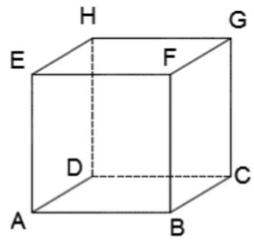
Titik sudut terbentuk dari pertemuan oleh tiga rusuk pada bangun ruang. Besar sudut pada bangun ruang kubus adalah siku-siku dengan besar 90⁰.

Sifat Bangun Ruang Kubus

Bangun ruang tiga dimensi kubus memiliki beberapa sifat khusus yang membedakannya dari bangun ruang lainnya sebagai berikut:

Terdapat 6 bidang berbentuk persegi dengan ukuran sama luas
Terdapat 12 rusuk yang ukurannya sama panjang
Terdapat 8 titik sudut berbentuk siku-siku dengan besar 90⁰
Mempunyai 12 diagonal bidang dengan ukuran panjang yang sama
Mempunyai 4 diagonal ruang

Kubus dalam Kehidupan Sehari-Hari

Benda dengan bentuk menyerupai kubus, yakni mempunyai 6 buah sisi sama panjang sangat mudah dijumpai dalam kehidupan sehari-hari. Salah satu contoh bangun berbentuk kubus yang mudah dijumpai adalah dadu untuk bermain monopoli atau ular tangga serta rubik.

Dadu yang memiliki mata dadu dari 1 sampai 6 menunjukkan sisi-sisinya yang ada 6 buah dengan ukuran sama sehingga merupakan kubus. Rubik yang digunakan untuk melatih kecerdasan otak juga merupakan contoh kubus. Kubus juga bisa ditemukan pada dus atau kotak kemasan yang semua sisi sama panjang.

Diagonal Sisi Kubus

Diagonal sisi kubus merupakan ruas garis yang menghubungkan dua titik sudut yang ada pada rusuk berbeda pada satu bidang sisi kubus.

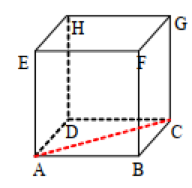
Dapat dilihat pada Gambar 2 di atas, garis merah putus-putus di bidang persegi ABCD merupakan diagonal sisi kubus ABCD.EFGH yang juga merupakan diagonal pada persegi. Bangun kubus mempunyai 12 diagonal sisi dengan ukuran yang sama karena setiap rusuk kubus memiliki panjang yang sama.

Bangun kubus memiliki 12 diagonal sisi yang bisa dihitung panjangnya menggunakan rumus phytagoras yakni:

d² = s² + s²
d² = 2s²
d = s√2

Keterangan:

d = diagonal sisi kubus
s = sisi kubus

Diagonal Ruang Kubus

Diagonal ruang kubus adalah ruas garis yang menghubungkan dua buah titik sudut yang saling berhadapan di dalam bangun kubus yang masing-masing terletak pada sisi atas dan sisi alas yang tidak berada pada satu bidang kubus.

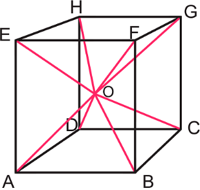
Diagonal kubus saling berpotongan di bagian tengah yang membagi kedua diagonal ruang sama panjang. Pada bangun kubus ABCD.EFGH di Gambar 3 di atas, terdapat 4 diagonal ruang yakni diagonal BH, DF, AG dan CE.

Bidang Diagonal Kubus

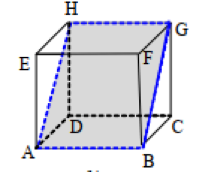
Bidang ABGH pada Gambar 4. di atas merupakan bidang diagonal kubus ABCD.EFGH. Bidang diagonal pada kubus adalah bidang yang melewati dua buah rusuk saling berhadapan serta melalui diagonal bidang sejajar yang saling berhadapan.

Bidang diagonal kubus membagi kubus menjadi dua bagian berukuran sama besar. Kubus mempunyai enam bidang diagonal berbentuk persegi panjang dimana ukuran panjangnya adalah diagonal sisi dari bangun kubus.

Jaring-Jaring Kubus

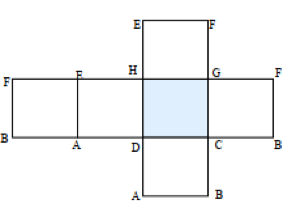
Jaring-jaring kubus adalah keenam sisi kubus yang dibuka atau direntangkan sehingga terlihat bentuk setiap sisinya. Pada Gambar 5. di atas terlihat bahwa sisi pada kubus berbentuk persegi. Bidang DCGH warna biru adalah sisi alasnya dengan sisi BAEF adalah atasnya.

Rumus Kubus

Luas Permukaan Kubus

Bidang tegak dan sisi alas kubus berbentuk persegi yang memiliki rusuk dengan panjang yang sama. Sehingga untuk menghitung luas permukaan kubus dapat dilakukan menjumlahkan total seluruh luas sisi persegi yang menjadi bidang pembatas kubus.

Kubus mempunyai 6 buah sisi sehingga untuk menghitung luas permukaan menggunakan rumus berikut:

Luas permukaan = 6 x s x s
Luas permukaan = 6 x s²

Volume Kubus

Volume kubus bisa dihitung dengan mengalikan semua sisi kubus yang mana berdasarkan rumus bangun ruang pada umumnya volume dihitung dengan mengalikan luas alas dan tinggi.

Pada kubus karena alas berbentuk persegi maka luas alas adalah perkalian sisi dengan sisi. Sementara ukuran tinggi kubus adalah sisi kubus tersebut.

V = luas alas x tinggi
V = s x s x s
V = s³

Diketahui:
s = sisi kubus

Pelajari Juga Balok

Soal dan Pembahasan

Sebuah dadu memiliki bentuk seperti gambar di bawah ini.

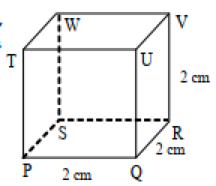
Tentukan beberapa hal berikut ini:

a. Sebutkan rusuk yang sejajar dengan rusuk di bawah ini:

b. Sebutkan sisi yang sejajar dengan:

sisi QRVU
sisi PQRS
sisi PQUT

c. Tentukan luas permukaan dan juga volume bangun dadu

Pembahasan

Diketahui:

Dadu berupa bangun kubus dengan panjang rusuk-rusuknya adalah 2 cm.

Jawab:

a. Rusuk yang sejajar dengan:

b. Sisi yang sejajar dengan:

c. Untuk menghitung luas permukaan kubus menggunakan rumus di bawah ini:

Lp = 6 x s²
Lp = 6 x 2²
Lp = 6 x 4
Lp = 24 cm²

Sehingga luas permukaan kubus sebesar 24 cm². Untuk menghitung volume kubus menggunakan rumus berikut ini:

V = s x s x s
V = s³
V = 2³
V = 8 cm³

Sehingga volume dadu yang berbentuk kubus sebesar 8 cm³

Kesimpulan

Kubus adalah bangun tiga dimensi yang memiliki 6 buah sisi sama panjang berbentuk persegi. Rusuk kubus ada 12 rusuk dengan ukuran sama panjang dan 8 titik sudut berbentuk siku-siku sebesar 90⁰. Mengingat keberadaan benda bentuk kubus banyak di sekitar, pemahaman materi kubus sangat penting.