Kerucut: Pengertian, Irisan, Jaring, Rumus, Contoh Soal

Pernah melihat topi ulang tahun yang banyak dipakai oleh anak-anak? Jika dilihat dengan teliti, maka bentuk topi ulang tahun tersebut mengadopsi bentuk bangun ruang kerucut. Bangun kerucut adalah bangun tiga dimensi yang hanya terdiri oleh dua bidang saja yakni sisi alas dan satu sisi tegak.

Pengertian Kerucut

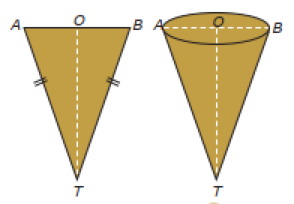
Kerucut terbentuk dari sebuah segitiga yang diputar pada sumbu tinggi segitiga tersebut sehingga membentuk alas kerucut berupa lingkaran. Pada Gambar 1. di bawah ini terlihat bahwa segitiga sama kaki ATB memiliki tinggi OT.

Apabila segitiga sama kaki ATB diputar pada sumbu OT, maka akan terbentuk bangun ruang kerucut seperti yang terlihat di sisi kanan. Kerucut hanya mempunyai satu titik sudut saja yakni pada titik puncaknya.

Unsur-Unsur Kerucut

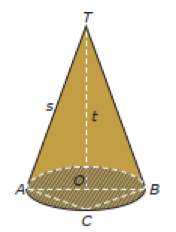
Pada Gambar 2. di atas bisa dilihat bahwa bangun ruang kerucut terdiri atas beberapa unsur yang membentuknya yakni:

• Bidang alas kerucut ditunjukkan pada Gambar 2. berbentuk lingkaran yang diarsir.
• Pusat lingkaran sebagai bidang alas kerucut ditunjukkan pada titik O sementara titik T merupakan puncak kerucut
• Jari-jari bidang alas kerucut yang berbentuk lingkaran ditunjukkan oleh ruas garis OA dan OB
• Diameter bidang alas kerucut berbentuk lingkaran ditunjukkan oleh ruas garis AB
• Tinggi kerucut (t) merupakan ruas garis yang menghubungkan titik O yang merupakan titik pusat lingkaran alas dan titik T sebagai titik puncak kerucut.
• Tali busur bidang alas kerucut ditunjukkan oleh ruas garis BC. Prinsip tali busur ini bisa ditemukan pada konsep lingkaran
• Selimut kerucut adalah sisi tegak kerucut yang menghubungkan titik puncak T dengan titik-titik pada lingkaran. Garis pelukis kerucut merupakan ruas-ruas garis yang menghubungkan keliling lingkaran pada titik puncak T.

Jaring-Jaring Kerucut

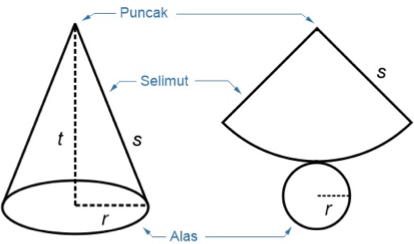
Apabila sebuah kerucut dipotong sepanjang ruas garis TB pada Gambar 2. di atas dan juga keliling alas lingkaran, maka terlihat bahwa kerucut tersebut terdiri dari sebuah lingkaran kecil sebagai alas dan ¼ bagian lingkaran yang lebih besar atau juring lingkaran.

Bagian-bagian kerucut berupa lingkaran sebagai alas dan juring lingkaran sebagai selimut merupakan jaring-jaring kerucut.

Irisan Kerucut

Irisan kerucut adalah kurva dua dimensi yang dibentuk oleh irisan pada bangun ruang kerucut oleh bidang dua dimensi. Ada empat jenis kurva dua dimensi yang terbentuk yakni parabola, lingkaran, hiperbola dan elips.

1. Parabola

Parabola merupakan tempat kedudukan titik-titik yang jaraknya terhadap garis tertentu atau disebut direktriks (d) dan jaranya terhadap titik tertentu yakni titik fokus (f) bernilai sama.

2. Hiperbola

Irisan berbentuk hiperbola pada bangun kerucut dihasilkan oleh bidang datar yang memotong dua buah kerucut.

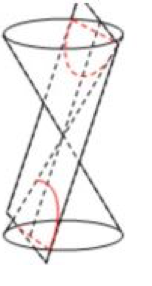
3. Elips

Irisan kerucut berbentuk elips dihasilkan oleh bidang datar yang memotong kerucut secara tidak tegak lurus dari garis sumbu utama.

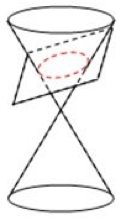
4. Lingkaran

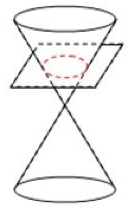
Lingkaran merupakan kruva dua dimensi yang terdiri dari titik-titik berjarak sama dari titik pusat lingkaran.

Pelajari Juga Lingkaran

Rumus Kerucut

• Luas Permukaan Kerucut

Untuk menghitung luas permukaan kerucut bisa dilihat dari jaring-jaring bangun kerucut yang ditunjukkan di Gambar 3. di atas. Dari gambar di atas terlihat bahwa panjang busur selimut kerucut sama dengan keliling dari alas kerucut.

Panjang busur selimut kerucut = keliling alas kerucut = 2 x π x r
Keliling lingkaran yang berjari-jari s = 2 x π x s
Luas lingkaran dengan jari-jari s adalah π x s²

Sehingga:
Luas selimut kerucut (juring lingkaran)/ Luas lingkaran = Panjang busur juring/Keliling lingkaran

Sehingga:
luas selimut kerucut (juring lingkaran) = {(2 x π x r)/ (2 x π x s)} x π x s²
luas selimut kerucut (juring lingkaran) = π x r x s

Dengan demikian untuk menghitung luas permukaan kerucut (Lp) menggunakan rumus di bawah ini:

Lp = Luas selimut kerucut + Luas alas kerucut berbentuk lingkaran
Lp = π x r x s + π x r²
Lp = π x r x (s + r)

Diketahui:

r = jari-jari lingkaran pada alas
s = garis pelukis kerucut
Lp = Luas permukaan kerucut

• Volume Kerucut

Sebagai sebuah bangun ruang, kerucut tentu memiliki volume yang bisa dihitung dengan mengalikan luas alas kerucut dengan tingginya kemudian dibagi 3.

V = 1/3 x π x r x r x t, atau
V = 1/3 x π x r²x t

Diketahui:

r = jari-jari lingkaran alas
t = tinggi kerucut (diukur dari tutuk pusat alas lingkaran ke titik puncak)
V = volume kerucut

Pelajari Juga Bangun Ruang

Contoh Soal

Bangun ruang kerucut dengan ukuran tinggi sebesar 10 cm dan diameter alas yakni 28 cm. Apabila nilai π = 22/7. Tentukan nilai berikut ini:

a. Luas selimut kerucut
b. Luas alas kerucut
c. Luas permukaan kerucut
d. Volume kerucut.

Kesimpulan

Kerucut adalah bangun ruang tiga dimensi yang terdiri dari dua bidang yakni sisi alas berbentuk lingkaran dan satu sisi tegak yang disebut selimut kerucut. Kerucut hanya mempunyai satu titik sudut saja yang ada di titik puncaknya. Topi ulang tahun adalah contoh benda yang menerapkan bentuk kerucut.