Ada berbagai jenis bilangan matematika yang dikenal, salah satu bilangan matematika yang banyak dimanfaatkan adalah bilangan prima. Meski banyak yang belum mengetahui, nyatanya mempelajari bilangan prima banyak memberikan manfaat dalam kehidupan sehari-hari terutama pada enskripsi data.
Definisi Bilangan Prima
Bilangan prima merupakan bilangan bulat positif yang hanya mempunyai dua faktor saja yakni bilangan 1 serta bilangan itu sendiri. Sebagai contoh g adalah bilangan prima maka bilangan tersebut hanya mempunyai dua faktor yakni g dan 1.
Bilangan prima termasuk ke dalam bilangan asli karena terdiri dari bilangan bulat positif dimulai dari 2, 3, 5, 7, … dan seterusnya. Perkembangan bilangan prima sendiri sudah dikenal sejak era sebelum Masehi oleh seorang ilmuwan matematika Yunani, yakni Euclid of Alexandria.
Penelitian mengenai bilangan prima terus berkembang hingga saat ini dengan ditemukannya angka prima terbesar yang dihitung menggunakan teknik perhitungan manual yakni 2127 – 1. Angka yang dihasilkan memiliki 39 digit dan dihitung oleh matematikawan Prancis bernama Edouard Lucas tahun 1876.
Selanjutnya penelitian mengenai bilangan prima terus berkembang hingga Gaorge Woltman dari Massachusetts Institute of Technology Amerika Serikat mendirikan proyek bernama the Great Internet Marsenne Prime Search (GIMPS).
Dari proyek ini ditemukan berbagai bilangan-bilangan prima yang belum ditemukan sebelumnya. Bilangan prima baru yang berhasil ditemukan adalah 282589933 – 1 yang menghasilkan total digit angka mencapai 24.862.048.
Bilangan Prima dalam Kehidupan Sehari-Hari
Bilangan prima sangat erat manfaatnya dalam kehidupan sehari-hari. Salah satu pemanfaatan utama dari aplikasi bilangan prima adalah dalam bidang teknologi komputasi. Bilangan prima bisa dimanfaatkan untuk membuat serta mengacak sebuah kunci dari susunan algoritma yang digunakan dalam aplikasi keamanan.
Bilangan prima berperan untuk menjaga keamanan akun sosial media sehingga akun sosial media tidak bisa dibajak oleh orang tidak bertanggung jawab. Bilangan prima juga biasa digunakan untuk membentuk pesan enkripsi yang berguna untuk menjaga keamanan dari kata sandi atau password elektronik.
Kata sandi atau password elektronik yang akan terjaga keamanannya menggunakan bilangan prima. Setiap pesan rahasia ataupun pesan melalui sosial media saat ini akan dienkripsi ke dalam suatu angka untuk mencegah terjadinya peretasan. Angka yang dihasilkan merupakan hasil kali 2 bilangan prima.
Pesan enkripsi akan dapat terbaca apabila sistem mengenali dua faktor bilangan prima yang sudah dikali. Oleh karena itu perkalian dua bilangan prima digunakan sebagai teknik pengamanan berbagai password, pin ATM, pesan rahasia dan pesan elektronik lainnya.
Contoh Bilangan Prima & Bukan Bilangan Prima
Bilangan prima terdiri dari bilangan-bilangan asli lebih dari 1. Angka 1 tidak termasuk bilangan prima karena 1 hanya mempunyai satu pembagi saja yakni angka 1 itu sendiri. Sementara angka 2 mempunyai dua faktor pembagi yakni 1 dan 2 (bilangan itu sendiri). Oleh karena itu 2 adalah bilangan prima.
Bilangan genap selain 2 bukan merupakan bilangan prima, misalnya 8, 10, 12 dan seterusnya. Hal ini dikarenakan bilangan genap tersebut memiliki lebih dari dua faktor pembagi yakni 1, 2, bilangan itu sendiri dan seterusnya sehingga tidak termasuk bilangan prima.
Misalnya bilangan 8 terdiri dari beberapa pembagi yakni 1, 2, 4, dan 8 sehingga bukan bilangan prima. Contoh yang lain yakni bilangan 16 yang memiliki beberapa faktor pembagi yaitu 1, 2, 4, 8, dan 16.
Untuk mencari bilangan prima, seorang matematikawan Prancis bernama Marin Mersenne menyusun suatu rumus yang cukup simpel untuk menghitungnya. Rumus mencari bilangan prima Mersenne adalah:
P = 2^n – 1
Lambang n merupakan bilangan prima sementara P adalah bilangan prima yang baru diperoleh. Sehingga apabila 2 dipangkatkan dengan suatu bilangan prima kemudian dikurang 1, maka bisa didapatkan bilangan prima. Berikut contoh perhitungan menggunakan rumus bilangan prima Mersenne:
P = 2^3 – 1 = 7 dimana 7 adalah bilangan prima.
Namun, setelah rumus Mersenne ini digunakan ternyata tidak semua bilangan P yang dihasilkan adalah bilangan prima. Misal jika nilai n yang dihitung adalah 11 dan 67 maka hasilnya bukan bilangan prima. Oleh karena itu harus dilakukan pengujian atau verifikasi saat melakukan perhitungan dengan rumus Mersenne.
Bilangan Prima 1 – 100
Seperti yang sudah dijelaskan sebelumnya di atas bahwa pada umumnya bilangan prima terdiri dari bilangan ganjil lebih dari 2. Meski begitu, tidak semua bilangan ganjil adalah bilangan prima karena bilangan 9 misalnya adalah bilangan ganjil namun tidak termasuk bilangan prima.
Bilangan prima kurang dari 100 sebenarnya tidak terlalu banyak sehingga mudah untuk diingat. Berikut tabel berisi daftar bilangan prima dari 1 sampai 100:
| 2 | 3 | 5 | 7 | 11 |
| 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 |
| 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 |
Mencari Faktor Prima Bilangan
Salah satu pembelajaran penting terkait bilangan prima adalah menghitung faktor prima bilangan. Faktor prima sendiri merupakan faktor dari suatu bilangan yang termasuk ke dalam bilangan prima. Ketika melakukan faktorisasi bilangan, maka faktorisasi bilangan tersebut selalu berhenti pada bilangan prima.
Untuk melakukan faktorisasi bilangan digunakan pohon faktor. Di bawah ini adalah contoh faktorisasi bilangan 30 menggunakan pohon faktor:
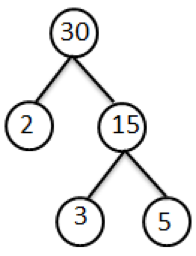
Bilangan yang tidak dapat diturunkan lagi dengan pohon faktor adalah bilangan prima yang merupakan faktor dari 30. Sehingga bisa disimpulkan bahwa faktorisasi prima dari 30 = 2 x 3 x 5 dengan faktor prima dari 30 adalah 2, 3 dan 5.
Pada penggunaan pohon faktor, apabila terdapat bilangan yang sama maka penulisan faktor prima hanya perlu dilakukan satu kali saja.
Soal dan Pembahasan Bilangan Prima
- Tentukan berapa faktor prima dari 27.
Jawab:
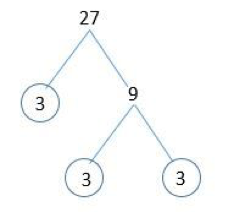
Faktorisasi prima dari 27 = 3 x 3 x 3 sehingga faktor prima dari 27 adalah 3.
- Tentukan berapa banyak faktor prima dari beberapa bilangan di bawah ini dan tentukan mana yang merupakan bilangan dengan dua faktor positif:
a. 300
b. 162
c. 233
d. 60
Jawab:
a. 300 = 2, 3, dan 5
b. 162 = 2 dan 3
c. 233 = 1 dan 233
d. 60 = 2, 3, dan 5
Maka bilangan 233 adalah bilangan prima karena hanya memiliki dua faktor saja yakni 1 dan dirinya sendiri yakni 233.
- Tentukan berapa bilangan prima yang ada di antara bilangan 100 sampai 120.
Jawab:
Bilangan prima antara 100 dan 120 ada 5 yaki 101, 103, 107, 109, 113.
Kesimpulan
Penggunaan bilangan prima memiliki manfaat yang sangat besar dalam kehidupan sehari-hari terutama sebagai pengamanan pesan terenkripsi. Bilangan prima adalah bilangan inti yang membentuk seluruh bilangan bulat karena bilangan bulat tersebut dapat dibentuk oleh sebuah faktor prima.
