Simpangan baku merupakan salah satu ukuran dalam statistika yang termasuk ke dalam ukuran penyebaran. Simpangan baku dikenal juga sebagai standar deviasi adalah ukuran penyebaran yang sangat baik karena dapat memberi gambaran penyebaran data di tiap unit observasi atau pengamatan.
Dengan menggunakan konsep standar deviasi atau simpangan baku, maka nilai-nilai data yang tersebar di dalam sekelompok data dapat diukur. Ukuran sebaran data ini sangat penting untuk menilai tingkat homogenitas di dalam suatu kelompok data atau sampel.
Pengertian
Simpangan baku secara sederhana dapat diartikan sebagai ukuran dalam statistika untuk melihat penyebaran angka di dalam sekelompok data. Untuk melihat sebaran data tersebut, maka nilai rata-rata atau mean digunakan sebagai tolok ukurnya.
Semakin dekat nilai individu suatu data dengan nilai rata-rata dari kelompok data tersebut, maka dapat disimpulkan bahwa nilai penyimpangannya juga semakin kecil. Sebaliknya apabila nilai individu suatu data dengan nilai rata-rata dari kelompok data tersebut semakin jauh, artinya penyimpangan semakin besar.
Simpangan baku atau yang sering disebut sebagai standar deviasi dihitung dengan mengakarkan kuadrat varians data dan menentukan simpangan atau deviasi setiap titik datanya relative terhadap rata-rata. Apabila data semakin tersebar, maka simpangan baku pun semakin besar.
Cara Mencari Nilai Simpangan Baku
Untuk mencari nilai simpangan baku ditentukan kepada jenis datanya apakah data kelompok atau data tunggal. Data tunggal adalah data yang disajikan secara lebih sederhana dan tidak dibedakan berdasarkan kelas-kelas interval.
Data tunggal hanya memuat satu jenis variabel saja yang diambil dari sekelompok objek populasi seperti data barang yang paling laku, data berat badan dan sebagainya. Berikut langkah untuk menghitung simpangan baku dari sekelompok data tunggal menggunakan langkah berikut ini.
- Pertama-tama dihitung nilai rata-rata data atau mean dari sekelompok data tunggal menggunakan rumus Mean
- Selanjutnya seluruh data tunggal tersebut dikurangi dengan nilai rata-rata atau Mean. Selanjutnya hasil pengurangan tersebut dikuadratkan.
- Setelah seluruh selisih data dikuadratkan, maka data tersebut kemudian dijumlahkan dan dibagi dengan banyak data yang ada
- Nilai penjumlahan data tersebut kemudian diakar kuadrat
Sementara data kelompok merupakan kumpulan data dalam jumlah besar sehingga dikelompokkan ke dalam beberapa interval kelas. Untuk memudahkan pembacaan data kelompok maka penyajiannya menggunakan kelas frekuensi.
Untuk menghitung simpangan baku dari data kelompok, berikut langkah pengerjaannya:
- Langkah pertama adalah mencari nilai rata-rata atau Mean dari data kelompok
- Selanjutnya kurangi nilai tengah dari kelas frekuensi data dengan nilai Mean. Hasil pengurangan data kemudian dikuadratkan
- Selanjutnya hasil kuadrat dari selisih data tersebut dikali dengan frekuensi dari kelas interval yang sedang dihitung (kelas interval ke-i)
- Seluruh nilai perhitungan dijumlahkan dan dibagi total datanya
- Nilai akhir yang didapatkan diakar kuadrat
Fungsi
Fungsi standar deviasi atau simpangan baku adalah untuk menentukan kondisi sebaran data di dalam sekelompok data sampel. Standar deviasi digunakan untuk melihat seberapa dekat titik-titik data setiap individu data dengan rata-rata nilai dari sampel data.
Para ahli statistika menggunakan perhitungan standar deviasi untuk menentukan apakah suatu sampel yang diambil dari sekelompok data dapat mewakili gambaran keseluruhan populasi. Pengambil sampel dari sekelompok data bukanlah pekerjaan yang mudah.
Memilih data yang tepat yang dapat mewakili populasi tentu sulit sehingga perhitungan standar deviasi dapat membantu memudahkan pemilihan sampel yang bisa mewakili.
Rumus
Rumus standar deviasi ditentukan oleh jenis datanya apakah jenis data populasi, data kelompok dan juga standar deviasi sampel. Kelompok data disebut sebagai data sampel apabila jumlah datanya n < 30. Untuk menghitung standar deviasi data sampel berikut rumusnya:
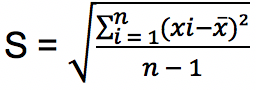
Keterangan:
S = standar deviasi atau simpangan baku data sampel
n = jumlah data
x = nilai mean rata-rata
xi = nilai data di urutan ke-i (i = 1, 2, 3, 4, 5, …)
Apabila jumlah data n > 30 maka data tersebut disebut sebagai data populasi. Untuk menghitung standar deviasi data populasi berikut rumusnya:
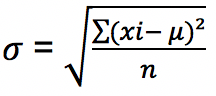
Keterangan:

Jika data disajikan menggunakan tabel distribusi frekuensi, maka data tersebut termasuk ke dalam data kelompok. Untuk menghitung standar deviasi data kelompok, maka nilai distribusi frekuensi harus diperhitungkan. Berikut rumus standar deviasi data kelompok:
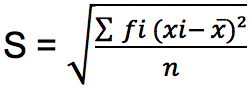
Keterangan:
S = standar deviasi atau simpangan baku data kelompok
n = jumlah data
x = mean atau nilai rata-rata
xi = nilai besaran data (i = 1, 2, 3, 4, 5, …)
fi = frekuensi kelompok
Contoh Soal & Pembahasan
- Soal 1
Beberapa data yang dikumpulkan terdiri dari data berikut ini: 32, 33, 35, 37, 39, 42, 45, 48, 48, 49. Tentukan berapa nilai standar deviasi atau simpangan baku dari data tersebut.
Jawab:
Pertama-tama nilai rata-rata atau Mean dihitung terlebih dahulu.
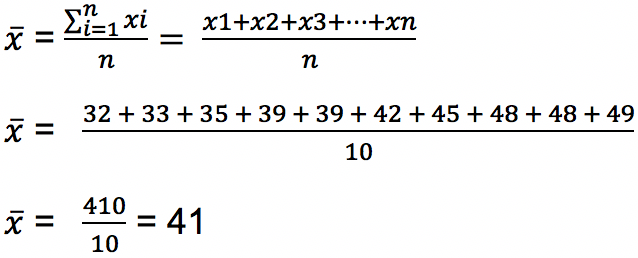
Kelompok data di atas termasuk data sampel karena jumlah datanya n < 30. Untuk menghitung standar deviasi data sampel berikut rumusnya:

- Soal 2
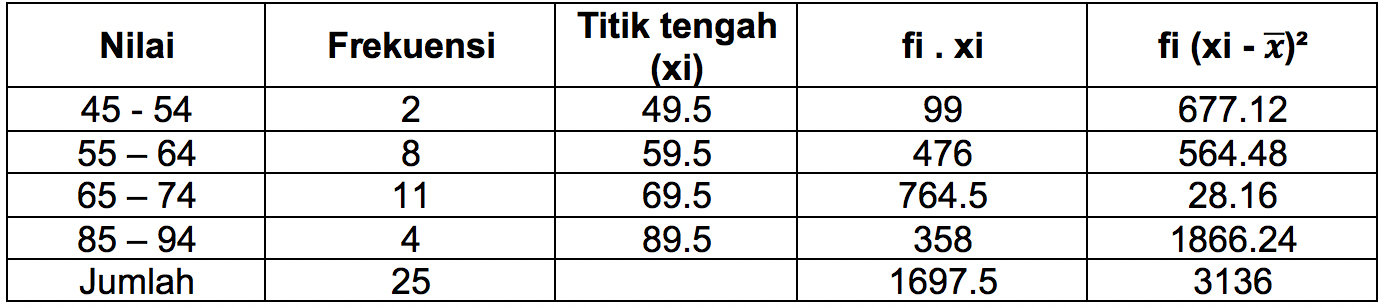
Nilai ujian IPA pelajar dikumpulkan dalam tabel di bawah ini.
| Nilai | Frekuensi |
| 45 – 54 | 2 |
| 55 – 64 | 8 |
| 65 – 74 | 11 |
| 85 – 94 | 4 |
Jawab:
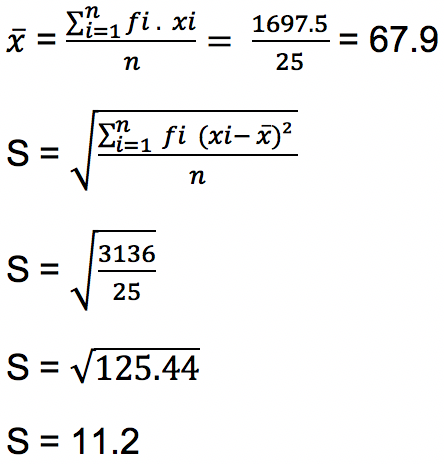
Simpangan baku atau standar deviasi adalah metode statistika yang berguna untuk melihat sebaran data dari sekelompok sampel serta menentukan simpangan data sampel ke rata-rata nilai sampel data. Standar deviasi bisa digunakan untuk jenis data tunggal maupun data kelompok.
