Garis dan sudut termasuk ke dalam materi dasar geometri di dalam Matematika. Memahami materi garis dan sudut sangat penting untuk bisa memahami konsep bangun datar, bidang, bangun ruang dan materi geometri lainnya.
Garis
Garis merupakan dasar dalam materi geometri. Semua benda di kehidupan sehari-hari tentu tersusun atas banyak garis. Garis dapat dibentuk ketika melewati setidaknya dua titik. Pada Gambar 1. di bawah bisa dilihat bahwa pada masing-masing ujung garis terdapat anak panah.
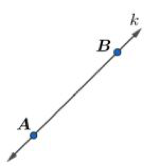
Tanda anak panah menunjukkan bahwa panjang garis tidak terbatas. Garis diberi nama sesuai dengan dua titik ujung yang dilewati garis tersebut. Misal pada Gambar 1 bisa diberi nama garis AB. Garis juga bisa diberi nama sesuai dengan symbol huruf kecil yang dituliskan seperti garis k.
Pengertian Garis
Secara sederhana, garis adalah kumpulan atau himpunan dari banyak titik yang saling berjejer dan terhubung secara kontinu.
Garis dalam Kehidupan Sehari-Hari
Tidak ada satupun bangun geometris yang tidak menerapkan konsep garis pada pembangunannya. Saat seorang arsitek membuat sketsa gambar, maka arsitektur tersebut banyak menerapkan garis. Garis adalah dasar dari setiap bangunan.
Sudut
Saat tukang memasang ubin berbentuk persegi pada lantai bangunan, ubin tersebut harus dipastikan dapat terpasang secara persis. Untuk memastikan ubin terpasang dengan benar, maka tukang akan menggunakan bantuan mistar siku-siku untuk mengukur setiap sudut ruangannya.
Selanjutnya garis lurus akan ditarik secara berpotongan menggunakan benang. Tujuannya untuk menyesuaikan dengan bentuk ubin berupa persegi. Karena bentuk ubin persegi maka artinya ada empat buah sudut siku-siku saling berhadapan.
Pengertian Sudut
Sudut dibentuk oleh dua buah garis lurus yang saling berpotongan pada satu titik yang sama. Setiap garis-garis yang membentuk suatu sudut disebut sebagai kaki sudut.
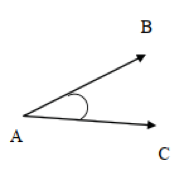
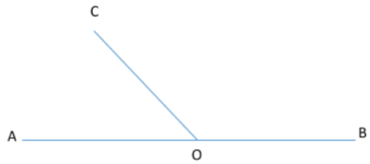
Pada Gambar 2. di atas dapat dilihat bahwa ruas garis AB dan ruas garis AC merupakan kaki sudut yang berpotongan di titik A. Titik A disebut sebagai titik sudut. Daerah yang dibatasi oleh kaki-kaki sudut merupakan daerah sudut. Besar sudut ditentukan oleh besar kecilnya bukaan kedua ruas kaki sudut.
Penamaan sudut bisa menggunakan titik sudutnya saja ataupun menggunakan tiga titik dari ruas kaki sudut dengan titik sudutnya di tengah. Misalnya pada sudut yang tampak di Gambar 2. bisa dinamai sebagai sudut BAC, sudut CAB atau sudut A.
Satuan untuk mengukur besar sudut adalah derajat (⁰). Besar sudut bisa diukur memakai busur derajat dengan besar sudut dalam sekali putaran adalah 360⁰.
Jenis-Jenis Sudut
- Sudut Lancip
Sudut lancip merupakan sudut yang memiliki ukuran besar sudut lebih kecil dari sudut siku-siku atau lebih kecil dari sudut 90⁰ namun lebih besar dari sudut 0⁰. Besar sudut lancip bisa dituliskan dengan lambang berikut ini:
0⁰ < x < 90⁰ (x merupakan besar sudut yang diukur)
- Sudut Siku-Siku
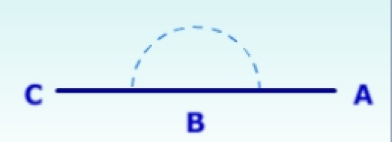
Sudut siku-siku merupakan sudut yang memiliki besar 90⁰. Sudut siku-siku dibentuk oleh dua kaki sudut yang berpotongan saling tegak lurus. Pada Gambar 3. di bawah ini terlihat bahwa kaki sudut BC tegak lurus dengan kaki sudut AB. Oleh karena itu sudut B merupakan sudut siku-siku.

Ada banyak bangun datar ataupun bangun ruang yang memiliki sudut siku-siku. Semua sudut dari bangun persegi serta persegi panjang adalah sudut siku-siku. Sementara pada bangun datar segitiga siku-siku hanya terdapat satu sudut siku-siku.
- Sudut Tumpul
Sudut tumpul merupakan sudut yang memiliki ukuran sudut lebih besar dari sudut siku-siku atau lebih besar dari sudut 90⁰ namun kurang dari sudut 180⁰. Besar sudut tumpul bisa dituliskan dengan lambang berikut ini:
90⁰ < x < 180⁰ (x merupakan besar sudut yang diukur)
Sudut tumpul memiliki nama obtuse angle dalam Bahasa Inggris. Beberapa jenis segitiga yang memiliki sudut tumpul adalah sudut segitiga sama kaki serta segitiga sama panjang.
Ada banyak bentuk sudut tumpul yang bisa ditemukan dalam kehidupan sehari-hari seperti atap rumah, kursi pantai, tongkat hockey dan boomerang.
- Sudut Lurus
Sudut lurus adalah jenis sudut yang dibentuk oleh satu garis lurus memanjang atau dua kaki sudut yang berbentuk horizontal dan saling bertemu di satu titik bagian tengah. Sudut lurus merupakan sudut yang memiliki besar 180⁰ di bagian tengahnya.
Sudut lurus berbeda dengan sudut yang memiliki besar 0⁰. Dalam Bahasa Inggris, sudut lurus disebut sebagai straight angle. Sudut lurus bisa ditemukan di berbagai benda di kehidupan sehari-hari yakni alas meja, jam di dinding yang menunjukkan jam 6 serta dinding tembok.
- Sudut Refleks
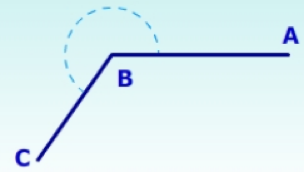
Sudut refleks merupakan jenis sudut yang memiliki besar sudut antara 180⁰ hingga 360⁰. Jika dilihat dari besar ukuran sudutnya, sudut refleks mempunyai ukuran sudut lebih besar dibandingkan sudut lancip, sudut siku-siku dan sudut tumpul. Besar sudut refleks bisa dituliskan dengan lambang berikut ini:
180⁰ < x < 360⁰ (x adalah besar sudut yang diukur)
Sudut ini dinamakan sudut refleks dikarenakan sudut ini adalah refleksi dari sudut tumpul.
Hubungan Antar Sudut
- Sudut Sehadap
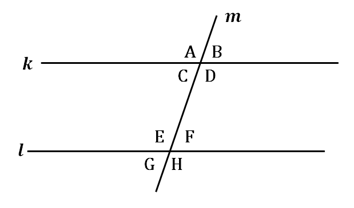
Sudut sehadap adalah sudut yang menghadap ke arah yang sama. Sudut sehadap mempunyai besar sudut yang sama. Sudut sehadap di Gambar 6. sebagai berikut:
- ∠A sehadap ∠E
- ∠B sehadap ∠F
- ∠C sehadap ∠G
- ∠D sehadap ∠H
- Sudut Dalam Sepihak
Sudut dalam sepihak saling berhadapan dengan total sudut 180⁰. Pada Gambar 6. sudut dalam sepihak adalah ∠C dan ∠E, ∠D dan ∠F
- Sudut Luar Sepihak
Sudut luar sepihak memiliki besar sudut 180⁰. Pada Gambar 6. sudut luar sepihak adalah ∠A dan ∠G, ∠B dan ∠H.
- Sudut Bertolak Belakang
Sudut bertolak belakang merupakan sudut dengan arah hadap berlawanan. Sudut ini dibentuk oleh dua perpanjangan garis yang sama yang berpotongan di titik tertentu sehingga membentuk pasangan sudut saling bertolak belakang. Besar sudut yang saling bertolak belakang adalah sama.
- Sudut Berpelurus
Sudut yang saling berpelurus (bersuplemen) memiliki besar sudut 180⁰. Pada gambar di bawah, sudut AOC adalah sudut berpelurus dari sudut BOC yang mana berlaku:
Sudut AOC + Sudut BOC = 180⁰
- Sudut Dalam Berseberangan
Sudut dalam berseberangan memiliki besar sudut yang sama. Pada Gambar 6. sudut dalam berseberangan adalah ∠C dan ∠F, ∠D dan ∠E.
- Sudut Luar Berseberangan
Sudut luar berseberangan memiliki besar sudut yang sama. Pada Gambar 6. sudut luar berseberangan adalah ∠A dan ∠H, ∠B dan ∠E.
Pelajari Juga Aturan Sinus Cosinus
Contoh Soal Garis dan Sudut
Jika ∠A1 = 115⁰ tentukan besar ∠B4
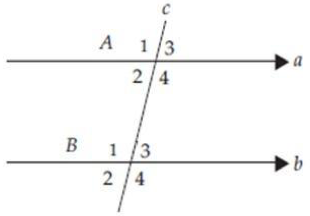
Jawab:
∠A1 dan ∠B4 adalah sudut luar berseberangan sehingga memiliki besar yang sama yaitu 115⁰
Ketika memberi nama sudut, maka akan dilihat tiga titik dari kaki-kaki sudut dengan titik sudutnya ada di tengah. Untuk memahami penggunaan sudut dan jenis-jenis sudut, perlu dipahami pengertian garis dan sudut.
