Hukum Kepler: Definisi, Fungsi, Rumus & Contoh Soal

Sejak masa Yunani Kuno atau bahkan sebelumnya, manusia sudah berusaha untuk memahami bagaimana kerja sistem tata surya. Saat membahas mengenai teori gravitasi, ternyata jauh sebelum hukum Newton terkait gravitasi muncul, ilmuwan bernama Johannes Keppler telah menyusun hukum Kepler.

Pengertian Hukum Kepler

Hukum Kepler disusun oleh ilmuwan bernama Johannes Keppler (1571 – 1630).  Johannes Keppler  sendiri termasuk salah satu ilmuwan di abad ke 16 Masehi yang membenarkan pendapat Heliosentris yakni bahwa matahari sebagai pusat tata surya.

Hukum Kepler berbicara mengenai pergerakan planet di tata surya dan keteraturan gerak planet tersebut. Pendapat Keppler sebenarnya selaras dengan pendapat Copernicus dimana gaya sebagai penyebab dari keteraturan gerak planet dalam tata surya.

Tanpa adanya gaya tersebut satelit di tata surya akan bergerak lurus dengan kecepatan yang tetap. Gaya gravitasi mempengaruhi gerakan planet dan benda angkasa di tata surya.

Keppler pun kemudian merumuskan 3 hukum peredaran benda di luar angkasa atau hukum Kepler untuk menyempurnakan pendapat heliosentris yang diambil.  

Hukum 1 Kepler

Hukum I Kepler berbicara mengenai bentuk lingkaran dari orbit-orbit planet. Bunyi hukum I Kepler yakni:

“Lintasan setiap planet yang bergerak mengelilingi matahari adalah lingkaran berbentuk elips dengan matahari yang terletak di salah satu dari titik fokusnya.”

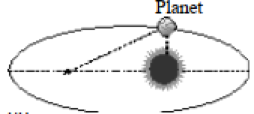
Hukum 2 Kepler

Hukum II Kepler berbicara mengenai kecepatan dari orbit planet yang mengitari matahari. Berikut bunyi hukum II Kepler:

“Setiap planet yang ada di tata surya bergerak sedemikian rupa sehingga suatu garis khayal yang apabila ditarik dari matahari menuju planet tersebut akan mencakup daerah dengan luas yang sama dalam waktu yang sama.”

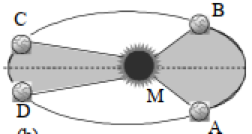
Berdasarkan skema hukum II Kepler di atas terlihat bahwa apabila garis AM ditarik kemudian digerakkan menyapu lurus sampai garis BM, maka luas yang terbentuk akan sama nilainya dengan luasan daerah yang disapu oleh garis CM sampai garis DM jika t_AB = t_CD

Berdasarkan hukum II Kepler juga dapat disimpulkan bahwa artinya planet harus bergerak lebih cepat ketika berada di titik A dan B dibandingkan ketika planet berada di titik C dan D.

Hukum 3 Kepler

Hukum III Kepler berbicara mengenai periode revolusi planet. Periode revolusi planet sangat dipengaruhi oleh jari-jari orbit rata-rata planet terhadap matahari. Berikut adalah bunyi dari Hukum III Kepler:

“Kuadrat dari periode planet yang mengitari matahari nilainya sebanding dengan pangkat tiga dari rata-rata orbit planet dari matahari.”

Munculnya hukum gravitasi Newton telah memperkuat teorema dalam hukum III Kepler atau sebaliknya, yakni hukum III Kepler akan memperkuat kebenaran hukum Newton tentang gravitasi.

Planet dapat bergerak terus-menerus mengelilingi matahari dan tidak lepas dari orbit perputaran planet karena adanya gaya sentripetal. Gaya sentripetal bersumber dari gaya gravitasi matahari sebagaimana yang ada pada hukum Newton.

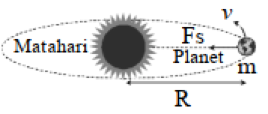
Berdasarkan Gambar 3. di atas, bisa diperoleh persamaan gaya sentripetal dan gaya gravitasi:

Fg = Fs

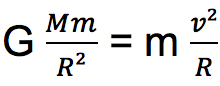
Kecepatan gerak planet bisa menggunakan rumus berikut:

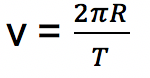
Jika rumus kecepatan gerak planet (v) disubstitusikan ke dalam persamaan gaya sentripetal dan gaya gravitasi di atas maka akan didapat hubungan sebagai berikut:

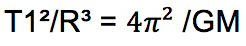
Nilai G dan M konstan sehingga dari persamaan di atas berlaku hukum:

T² ~ R³

Fungsi Hukum Kepler

1. Memperkirakan Lintasan Planet

Hukum Kepler di kehidupan modern memiliki fungsi untuk memperkirakan lintasan planet atau benda luar angkasa yang bergerak dengan mengorbit matahari seperti halnya asteroid serta planet-planet luar yang belum ditemukan ketika Johannes Keppler masih hidup.

Selain digunakan untuk memperkirakan lintasan planet atau benda angkasa saat mengorbit matahari, hukum Kepler juga digunakan untuk melihat orbit lain selain matahari seperti bulan yang mengorbit terhadap bumi.

2. Menemukan Keberadaan Benda Angkasa

Dengan menggunakan dasar dari hukum Kepler, para antariksawan dapat menemukan benda luar angkasa baru yang mengorbit planet di tata surya termasuk bumi. Dengan penelitian yang mendalam berkat bantuan hukum Kepler, ditemukan keberadaan benda baru yang mengorbit planet bumi selain bulan.

Benda yang mengorbit bumi ini adalah asteroid dengan ukuran 150 meter yang diberi nama Asteroid 2014 OL339. Asteroid ini terletak cukup dekat dengan planet Bumi sehingga tampak seperti satelit bumi. Orbit asteroid ini berbentuk elips.

3. Hukum Kepler Menguatkan Paham Heliosentris

Pada masa Yunani Kuno, para filsuf berpikiran bahwa bumi merupakan pusat dari tata surya. Salah satunya adalah Aristoteles yang merupakan seorang filsuf Yunani Kuno mengeluarkan teori geosentris (bumi sebagai pusat tata surya).

Kehadiran teori Hukum Kepler telah mematahkan pemahaman geosentris dan menggantinya dengan pemahaman heliosentris (matahari sebagai pusat tata surya).

Rumus Hukum Kepler

1. Rumus Hukum III Kepler

Bunyi dari Hukum 3 Kepler dapat dirumuskan sesuai dengan rumus berikut ini:

(T1/T2)² = (R1/R2)³

Keterangan:

T1 = Periode planet pertama
T2 = Periode planet kedua
R1 = Jarak planet yang pertama terhadap matahari
R2 = Jarak planet kedua terhadap matahari

2. Rumus Kecepatan Rata-Rata

η = 2 π/P

Keterangan:

η = kecepatan rata-rata
P = Periode planet (Revolusi)

3. Rumus Luas Orbit Elips

A = πab

Keterangan:

A = Luas orbit (m²)
a = jarak titik pusat elips dihitung ke orbit paling jauh (m)
b = jarak titik pusat elips dihitung menuju orbit paling dekat (m)

Contoh Soal Hukum Kepler

• Contoh 1

Planet Jupiter mempunyai jarak orbit ke matahari yang besarnya diperkirakan sama dengan 4 kali jarak orbit bumi ke matahari. Periode revolusi bumi ketika mengelilingi matahari secara penuh adalah 1 tahun. Tentukan berapa periode planet Jupiter dalam mengelilingi matahari.

• Contoh 2

Diketahui bawah pada sistem tata surya diketahui data jarak rata-rata bumi ke matahari sebesar 1 astronomi serta periode revolusi bumi sebesar 365 hari. Apabila jarak rata-rata Mars ke matahari sebesar 1,12 astronomi, tentukan periode revolusi Mars?

Hukum Kepler yang berbicara mengenai pergerakan benda-benda seperti planet dan satelit di tata surya memiliki fungsi yang sangat besar dalam kehidupan modern saat ini. Hukum Kepler digunakan untuk memperkirakan lintasan planet dan benda luar angkasa. Hukum Kepler dirumuskan ke dalam 3 hukum.